Exam 9: One-Sample Tests of Hypothesis
Exam 1: What Is Statistics79 Questions
Exam 2: Describing Data: Frequency Tables, Frequency Distributions, and Graphic Presentation87 Questions
Exam 3: Describing Data: Numerical Measures191 Questions
Exam 4: A Survey of Probability Concepts130 Questions
Exam 5: Discrete Probability Distributions121 Questions
Exam 6: Continuous Probability Distributions143 Questions
Exam 7: Sampling Methods and the Central Limit Theorem78 Questions
Exam 8: Estimation and Confidence Intervals134 Questions
Exam 9: One-Sample Tests of Hypothesis139 Questions
Exam 10: Two-Sample Tests of Hypothesis103 Questions
Exam 11: Analysis of Variance97 Questions
Exam 12: Linear Regression and Correlation166 Questions
Exam 13: Multiple Regression and Correlation Analysis128 Questions
Exam 14: Chi-Square Applications126 Questions
Exam 15: Index Numbers93 Questions
Exam 16: Time Series and Forecasting90 Questions
Exam 17: An Introduction to Decision Theory54 Questions
Select questions type
If the alternate hypothesis states that does not equal 4,000, what is the rejection region for the hypothesis test?
Free
(Multiple Choice)
4.9/5  (42)
(42)
Correct Answer:
A
If = 0.05, what is the probability of making a Type I error?
Free
(Multiple Choice)
4.8/5  (30)
(30)
Correct Answer:
B
If 20 out of 50 students sampled live in a college dormitory, what is the estimated proportion of students at the University living in a dormitory?
Free
(Multiple Choice)
4.9/5  (40)
(40)
Correct Answer:
B
A manufacturer of stereo equipment introduces new models in the fall. Retail dealers are surveyed immediately after the Christmas selling season regarding their stock on hand of each piece of equipment. It has been discovered that unless 40% of the new equipment ordered by the retailers in the fall had been sold by Christmas, immediate production cutbacks are needed. The manufacturer has found that contacting all of the dealers after Christmas by mail is frustrating as many of them never respond. This year 80 dealers were selected at random and telephoned regarding a new receiver. It was discovered that 38% of those receivers had been sold. Since 38% is less than 40%, does this mean that immediate production cutbacks are needed or can this difference of 2 percentage points be attributed to sampling? Test at the 0.05 level. Computed z = -0.37.
(Multiple Choice)
4.8/5  (36)
(36)
Given: null hypothesis is that the population mean is 16.9 against the alternative hypothesis that the population mean is not equal to 16.9. A random sample of 16 items results in a sample mean of 17.1 and the sample standard deviation is 2.4. It can be assumed that the population is normally distributed. Determine the observed "t" value.
(Multiple Choice)
4.9/5  (31)
(31)
Given: null hypothesis is that the population mean is 16.9 against the alternative hypothesis that the population mean is not equal to 16.9. A random sample of 25 items results in a sample mean of 17.1 and the sample standard deviation is 2.4. It can be assumed that the population is normally distributed. Determine the observed "t" value.
(Multiple Choice)
4.9/5  (46)
(46)
Based on the Nielsen ratings, the local CBS affiliate claims its 11:00 PM newscast reaches 41% of the viewing audience in the area. In a survey of 100 viewers, 36% indicated that they watch the late evening news on this local CBS station. What is the z-statistic?
(Multiple Choice)
4.9/5  (33)
(33)
A restaurant that bills its house account monthly is concerned that the average monthly bill exceeds $200 per account. A random sample of twelve accounts is selected, resulting in a sample mean of $220 and a standard deviation of $12. The t-test is to be conducted at the 5% level of significance.
(Multiple Choice)
4.8/5  (32)
(32)
The Jamestown Steel Company manufactures and assembles desks and other office equipment at several plants. The weekly production of the Model A325 desk follows a normal probability distribution, with a mean of 200 and a standard deviation of 16. Recently, due to market expansion, new production methods have been introduced and new employees hired. The vice president of manufacturing would like to investigate whether there has been an increase in the weekly production of the Model A325 desk. The mean number of desks produced last year (50 weeks, because the plant was shut down two weeks for vacation) is 203.5. Is the mean number of desks increased from 200? Test using the.10 significance level. 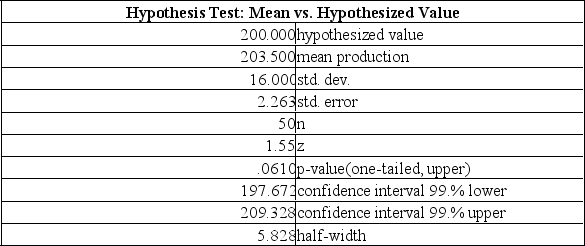
(Multiple Choice)
4.7/5  (34)
(34)
It is claimed that in a bushel of peaches less than ten percent are defective. A sample of 400 peaches is examined and 50 are found to be defective. What is the sample proportion?
(Multiple Choice)
4.9/5  (34)
(34)
A nationwide survey of college students was conducted and found that students spend two hours per class hour studying. A professor at your school wants to determine whether the time students spend at your school is significantly different from the two hours. A random sample of fifteen statistics students is carried out and the findings indicate an average of 1.75 hours with a standard deviation of 0.24 hours.
(Multiple Choice)
4.8/5  (49)
(49)
The average cost of tuition, room and board at community colleges is reported to be $11,500 per year, but a financial administrator believes that the average cost is higher. A study conducted using 150 community colleges showed that the average cost per year is $12,000 with a standard deviation of $1,200. Let = 0.05. What are the null and alternative hypotheses for this study?
(Multiple Choice)
4.8/5  (33)
(33)
The mean weight of newborn infants at a community hospital is said to be 6.6 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6 pounds. Does this sample support the original claim? The null hypothesis is:
(Multiple Choice)
4.9/5  (32)
(32)
The mean length of a small counter balance bar is 43 millimeters. There is concern that the adjustments of the machine producing the bars have changed. Test the claim at the 0.02 level that there has been no change in the mean length. The alternate hypothesis is that there has been a change. Twelve bars (n = 12) were selected at random and their lengths recorded. The lengths are (in millimeters) 42, 39, 42, 45, 43, 40, 39, 41, 40, 42, 43 and 42. The mean of the sample is 41.5 and the standard deviation 1.784. Computed t = -2.913. Has there been a statistically significant change in the mean length of the bars?
(Multiple Choice)
4.7/5  (28)
(28)
The mean weight of newborn infants at a community hospital is said to be 6.6 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6 pounds. What are the degrees of freedom associated with this claim?
(Multiple Choice)
4.9/5  (39)
(39)
i. For a one-tailed test using the 0.05 level of significance, the critical value for the z test is 1.645, but for t it is 1.96. ii. For a one-tailed test using the 0.01 level of significance, the critical value for the z-test is 1.645, but for t it is 1.96.
iii. For a two-tailed test using the 0.05 level of significance the critical value for the z-test is 1.96 and it is the same for the t-test.
(Multiple Choice)
4.9/5  (35)
(35)
i. If the null hypothesis is 200 and the alternate hypothesis states that is less than 200, then, a two-tail test is being conducted. ii. For a one-tailed test of hypothesis, the area of rejection is only in one tail of the curve.
iii. As the sample size increases, the curve of the t-distribution approaches the standard normal distribution
(Multiple Choice)
4.8/5  (34)
(34)
It is claimed that in a bushel of peaches less than ten percent are defective. A sample of 400 peaches is examined and 50 are found to be defective. If = 0.025, what will be the decision?
(Multiple Choice)
4.7/5  (32)
(32)
If the 1% level of significance is used and the computed value of z is +6.00, what is our decision?
(Multiple Choice)
5.0/5  (37)
(37)
The mean weight of newborn infants at a community hospital is said to be 6.6 pounds. A sample of seven infants is randomly selected and their weights at birth are recorded as 9.0, 7.3, 6.0, 8.8, 6.8, 8.4, and 6.6 pounds. Does this sample support the original claim? What is the decision for a significant increase in the average birthrate at a 5% level of significance? 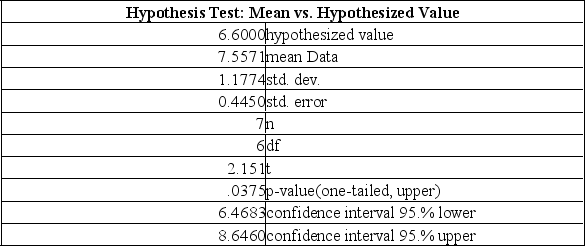
(Multiple Choice)
4.9/5  (39)
(39)
Showing 1 - 20 of 139
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)