Exam 4: Linear Programming
Exam 1: Urban Services107 Questions
Exam 2: Business Efficiency104 Questions
Exam 3: Planning and Scheduling108 Questions
Exam 4: Linear Programming111 Questions
Exam 5: Exploring Data: Distributions115 Questions
Exam 6: Exploring Data: Relationships104 Questions
Exam 7: Data for Decisions99 Questions
Exam 8: Probability: the Mathematics of Chance108 Questions
Exam 9: Social Choice: the Impossible Dream103 Questions
Exam 10: The Manipulability of Voting Systems106 Questions
Exam 11: Weighted Voting Systems111 Questions
Exam 12: Electing the President93 Questions
Exam 13: Fair Division121 Questions
Exam 14: Apportionment112 Questions
Exam 15: Game Theory: the Mathematics of Competition113 Questions
Exam 16: Identification Numbers110 Questions
Exam 17: Information Science94 Questions
Exam 18: Growth and Form111 Questions
Exam 19: Symmetry and Patterns115 Questions
Exam 20: Tilings112 Questions
Exam 21: Savings Models113 Questions
Exam 22: Borrowing Models113 Questions
Exam 23: The Economics of Resources119 Questions
Select questions type
The graph of the feasible region for a mixture problem is shown below. Find the point that maximizes the profit function P = 2x + y. 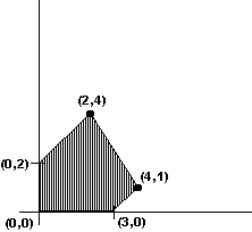
(Multiple Choice)
4.7/5  (42)
(42)
What type of solution does the Northwest Corner Rule produce for the transportation problem?
(Short Answer)
4.8/5  (28)
(28)
Find the point of intersection for the lines represented by the equations 2x + 4y = 12 and 3x + y = 13.
(Short Answer)
4.7/5  (33)
(33)
Write the resource constraints for this situation: Kim and Lynn produce tables (x) and chairs (y). Each piece is assembled, sanded, and stained. A table requires two hours to assemble, three hours to sand, and three hours to stain. A chair requires four hours to assemble, two hours to sand, and three hours to stain. The profit earned on each table is $20 and on each chair is $12. Together Kim and Lynn spend at most 16 hours assembling, 10 hours sanding, and 13 hours staining.
(Multiple Choice)
4.9/5  (30)
(30)
An optimal solution for a linear programming problem will always occur at a corner point of the feasible region.
(True/False)
4.9/5  (39)
(39)
The feasible region for a linear programming mixture problem with two products is in the first quadrant of the Cartesian plane.
(True/False)
4.9/5  (35)
(35)
Given below is the sketch of the feasible region in a linear programming problem. Which point is NOT in the feasible region? 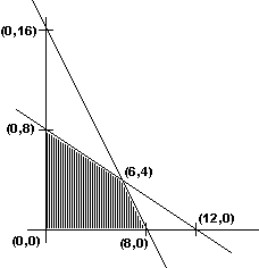
(Multiple Choice)
4.9/5  (27)
(27)
Suppose the feasible region has five corners, at these points: (1, 1), (1, 7), (5, 7), (5, 5), and (4, 3). If the profit formula is P = $5x $2y, which point maximizes the profit?
(Multiple Choice)
4.8/5  (27)
(27)
The feasible region for a linear programming mixture problem may have holes in it.
(True/False)
4.7/5  (34)
(34)
Graph the feasible region identified by the inequalities: 2x+3y\leq12 1x+5y\leq10 x\geq0,y\geq0
(Multiple Choice)
4.8/5  (41)
(41)
Find the point of intersection for the lines represented by the equations 3x + 2y = 14 and 4x + 5y = 28.
(Short Answer)
4.8/5  (38)
(38)
Use the following to answer the Questions:
concern the following tableau for a shipping problem. 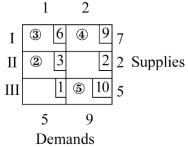 -In the optimal solution, how many units are shipped from supplier I to customer 2?
-In the optimal solution, how many units are shipped from supplier I to customer 2?
(Short Answer)
5.0/5  (31)
(31)
Refer to the feasible region defined by the following constraints to answer the following questions :
x+y\leq6 x+2y\leq8 x\geq0 y\geq0
-If the profit formula is what is the maximum profit?
(Multiple Choice)
4.9/5  (23)
(23)
Suppose the feasible region has four corners, at these points: (0, 0), (8, 0), (0, 12), and (4, 8). For which of these profit formulas is the profit maximized, producing a mix of products at (4, 8)?
(Multiple Choice)
4.9/5  (31)
(31)
Use the following tableau to answer the questions:
concern the following tableau for a shipping problem. 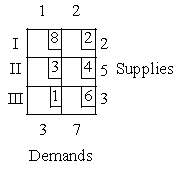 -What is the cost for the optimal solution to this shipping problem?
-What is the cost for the optimal solution to this shipping problem?
(Multiple Choice)
4.7/5  (39)
(39)
Given below is the sketch of the feasible region in a linear programming problem. Which point is NOT in the feasible region? 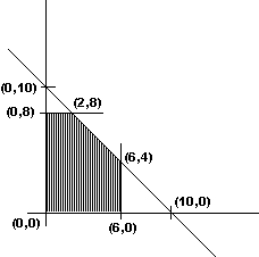
(Multiple Choice)
4.7/5  (28)
(28)
Write a profit formula for this mixture problem: A company manufactures patio chairs (x) and rockers (y). Each piece is made of wood, plastic, and aluminum. A chair requires one unit of wood, one unit of plastic, and two units of aluminum. A rocker requires one unit of wood, two units of plastic, and five units of aluminum. The company's profit on a chair is $7 and on a rocker is $12. The company has available 400 units of wood, 500 units of plastic, and 1450 units of aluminum.
(Multiple Choice)
4.8/5  (40)
(40)
Showing 61 - 80 of 111
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)