Exam 15: Game Theory: the Mathematics of Competition

Use the following information to answer Questions The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense. Defense Run Pass Offense Run 0.5 0.6 Pass 0.8 0.4 -In such situations, what is the optimal solution for the offense?

Use the following information to answer the Questions: In American football the "third down and short" situation occurs often. The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense. Defense Run Pass Offense Run 0.2 0.8 Pass 0.5 0.1 -What is the optimal mixed strategy for the defense?

Describe a saddlepoint of a zero-sum game for two players where the payoff matrix represent gains to the row player I and losses to column player II.

In the following game of batter-versus-pitcher in baseball, the batter's batting averages are shown in the game matrix: Solve the game, determining the best mix of selections for both batter and pitcher.

In the following game of batter-versus-pitcher in baseball, the batter's batting averages are shown in the game matrix. 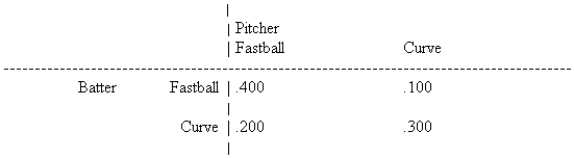What is the batter's optimal strategy?

Consider the following partial-conflict game played in a noncooperative manner. The first payoff is to player I; the second is to player II. $\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\quad$$\text { Player II }$ Player I Choice A Choice B Choice A (3,4) (5,5) Choice B (4,1) (6,2) What outcomes constitute a Nash equilibrium?

Consider the following partial-conflict game played in a noncooperative manner. The first payoff is to player I; the second is to player II. Player II Player I Choice A Choice B Choice A (6,1) (3,3) Choice B (5,5) (1,6) Discuss the players' possible strategies when this game is played.

What is the name of a table whose rows and columns correspond to the strategies of the two players?

Suppose on a committee of three people Kim (the chair), Chris, and Terry each have one vote, but Kim breaks any tie. In attempting to elect someone to drive the van, each person has a priority list: \mid Kim's Priorities Chris's Priorities Terry's Priorities 1st choice \mid Chris Kim Terry 2nd choice \mid Kim Chris Chris 3rd choice \mid Terry Terry Kim Which of the following are Nash equilibria? I: Every person votes for Chris. II: Every person votes for his/her second choice.

In a truel where the choices are sequential, what is the optimal strategy for the first player?

In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to the column player II. Does this game have a saddlepoint? What is each player's minimax or maximin strategy? $\left[ \begin{array} { l l l } 2 & 8 & 6 \\7 & 5 & 1 \\6 & 8 & 9\end{array} \right]$

The value of a zero-sum game is a saddlepoint.

Use the following information to answer the Questions: In American football the "third down and short" situation occurs often. The probabilities of obtaining a first down, shown below, are dependent on the choice of the offense and the anticipated choice of the defense. Defense Run Pass Offense Run 0.2 0.8 Pass 0.5 0.1 -Suppose the value of the game is $p$ What does this mean for the defense?

Every "zero-sum" game is a "fair" game.

In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to the column player II. $\left[ \begin{array} { l l l l } 8 & 1 & 5 & 2 \\5 & 4 & 7 & 8 \\1 & 3 & 4 & 5 \\8 & 4 & 3 & 5\end{array} \right]$ The minimax strategy of player II is:

In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to the column player II. $\left[ \begin{array} { l l l l } 8 & 1 & 5 & 2 \\5 & 4 & 7 & 8 \\1 & 3 & 4 & 5 \\8 & 4 & 3 & 5\end{array} \right]$ The maximin strategy of player I is:

In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to the column player II. $\left[ \begin{array} { l l l } 5 & 8 & 6 \\4 & 3 & 1 \\2 & 6 & 7\end{array} \right]$ Which of the following statements is true?

In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II. The minimax strategy of player II is:

In the following two-person zero-sum game, the payoffs represent gains to the row player I and losses to column player II. 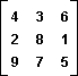The maximin strategy of player I is:

Use the following information to answer the Questions: 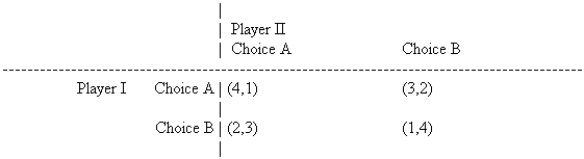-Assume that the game is played continually, and players can change their choices at noon each day. If the game begins with both players selecting choice A, what should happen at the first opportunity to change?