Exam 13: Introduction to Optimization Modeling
Exam 1: Introduction to Data Analysis and Decision Making30 Questions
Exam 2: Describing the Distribution of a Single Variable97 Questions
Exam 3: Finding Relationships Among Variables84 Questions
Exam 4: Probability and Probability Distributions113 Questions
Exam 5: Normal, binomial, poisson, and Exponential Distributions118 Questions
Exam 6: Decision Making Under Uncertainty106 Questions
Exam 7: Sampling and Sampling Distributions92 Questions
Exam 8: Confidence Interval Estimation85 Questions
Exam 9: Hypothesis Testing85 Questions
Exam 10: Regression Analysis: Estimating Relationships97 Questions
Exam 11: Regression Analysis: Statistical Inference87 Questions
Exam 12: Time Series Analysis and Forecasting104 Questions
Exam 13: Introduction to Optimization Modeling91 Questions
Exam 14: Optimization Modeling: Applications115 Questions
Exam 15: Introduction to Simulation Modeling81 Questions
Exam 16: Simulation Models104 Questions
Select questions type
When formulating a linear programming spreadsheet model,there is one target (objective)cell that contains the value of the objective function.
(True/False)
4.8/5  (39)
(39)
When formulating a linear programming spreadsheet model,we specify the constraints in a Solver dialog box,since Excel does not show the constraints directly.
(True/False)
4.8/5  (33)
(33)
If a constraint has the equation 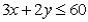 ,then the constraint line passes through the points (0,20)and (30,0):
,then the constraint line passes through the points (0,20)and (30,0):
(True/False)
4.7/5  (41)
(41)
In some cases,a linear programming problem can be formulated such that the objective can become infinitely large (for a maximization problem)or infinitely small (for a minimization problem).This type of problem is said to be:
(Multiple Choice)
4.9/5  (36)
(36)
If a manufacturing process takes 3 hours per unit of x and 5 hours per unit of y and a maximum of 100 hours of manufacturing process time are available,then an algebraic formulation of this constraint is:
(Multiple Choice)
4.9/5  (33)
(33)
Linear programming models have three important properties.They are:
(Multiple Choice)
4.9/5  (37)
(37)
There are two primary ways to formulate a linear programming problem,the traditional algebraic way and in spreadsheets.
(True/False)
4.8/5  (34)
(34)
Reduced costs indicate how much the objective coefficient of a decision variable that is currently 0 or at its upper bound must change before that the value of that variable changes.
(True/False)
4.9/5  (41)
(41)
It helps to ensure that Solver can find a solution to a linear programming problem if the model is well-scaled; that is,all of the numbers are of roughly the same magnitude.
(True/False)
4.8/5  (41)
(41)
All linear programming problems should have a unique solution,if they can be solved.
(True/False)
4.9/5  (33)
(33)
One of the things that you can do with linear programming and a spreadsheet model is to develop a user interface to make it easier for someone who is not an expert in using linear programming.The output can be a report that explains the optimal policy in non-technical terms.The type of system being described is called a (n):
(Multiple Choice)
4.8/5  (50)
(50)
The additivity property of LP models implies that the sum of the contributions from the various activities to a particular constraint equals the total contribution to that constraint.
(True/False)
4.9/5  (46)
(46)
There is often more than one objective in linear programming problems
(True/False)
4.8/5  (33)
(33)
The divisibility property of linear programming means that a solution can have both:
(Multiple Choice)
5.0/5  (40)
(40)
Write out an algebraic expression for the objective function in this problem.
(Short Answer)
4.8/5  (42)
(42)
If a solution to an LP problem satisfies all of the constraints,then is must be feasible.
(True/False)
4.7/5  (38)
(38)
Consider the following linear programming problem: Maximize 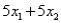 Subject to
Subject to 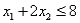
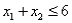
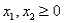 The above linear programming problem:
The above linear programming problem:
(Multiple Choice)
4.8/5  (37)
(37)
Showing 21 - 40 of 91
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)