Exam 13: Introduction to Optimization Modeling
Exam 1: Introduction to Data Analysis and Decision Making30 Questions
Exam 2: Describing the Distribution of a Single Variable97 Questions
Exam 3: Finding Relationships Among Variables84 Questions
Exam 4: Probability and Probability Distributions113 Questions
Exam 5: Normal, binomial, poisson, and Exponential Distributions118 Questions
Exam 6: Decision Making Under Uncertainty106 Questions
Exam 7: Sampling and Sampling Distributions92 Questions
Exam 8: Confidence Interval Estimation85 Questions
Exam 9: Hypothesis Testing85 Questions
Exam 10: Regression Analysis: Estimating Relationships97 Questions
Exam 11: Regression Analysis: Statistical Inference87 Questions
Exam 12: Time Series Analysis and Forecasting104 Questions
Exam 13: Introduction to Optimization Modeling91 Questions
Exam 14: Optimization Modeling: Applications115 Questions
Exam 15: Introduction to Simulation Modeling81 Questions
Exam 16: Simulation Models104 Questions
Select questions type
If the objective function has the equation 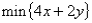 ,then the slope of the objective function line is 2:
,then the slope of the objective function line is 2:
(True/False)
4.8/5  (38)
(38)
Proportionality,additivity,and divisibility are three important properties that LP models possess,which distinguish them from general mathematical programming models:.
(True/False)
4.8/5  (39)
(39)
Suppose the allowable increase and decrease for shadow price for a constraint are $25 (increase)and $10 (decrease).If the right hand side of that constraint were to increase by $10 the optimal value of the objective function would change.
(True/False)
4.9/5  (33)
(33)
(A)What is the objective function in this problem?
(B)What are the constraints in this problem? Write an algebraic expression for each.
(C)Find an optimal solution to the problem using the formulation given in (A)and (B).What is the call plan,and what is the total cost?
(D)Implement the model in (C)in Excel Solver and obtain an answer report.Which constraints are binding on the optimal solution?
(E)Obtain a sensitivity report for the model in (D).If the professor could cut the cost of evening calls from $4 to $3,what would the new calling plan be?
(F)Again using the sensitivity report obtained for (E),suppose the professor could get by with just 100 calls for single females.What would the call costs be in that case? Explain your answer.
(Essay)
4.9/5  (36)
(36)
There are generally two steps in solving an optimization problem,model development and optimization.
(True/False)
4.8/5  (36)
(36)
If the objective function has the equation 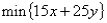 ,then the y-intercept of the objective function line is 40:
,then the y-intercept of the objective function line is 40:
(True/False)
4.9/5  (41)
(41)
(A)Formulate a linear programming model that will enable the farmer to determine the number of acres that should be planted cotton and/or corn in order to maximize his profit.
(B)Find an optimal solution to the model in (A)and determine the maximum profit.
(C)Implement the model in (A)in Excel Solver and obtain an answer report.Which constraints are binding on the optimal solution?
(D)Obtain a sensitivity report for the model in (A).How much should the farmer be willing to pay for an additional worker?
(E)Suppose the farmer hires 10 additional workers.Can you use the sensitivity analysis obtained for (D)to determine his expected profit? Would his planting plan change? Explain your answer.
(F)Suppose the farmer now wants to hire 20 additional workers,instead of just 10.Can you use the sensitivity analysis obtained for (D)to determine his expected profit? Explain your answer.
(Essay)
4.9/5  (43)
(43)
In general,the complete solution of a linear programming problem involves three stages: formulating the model,invoking Solver to find the optimal solution,and performing sensitivity analysis.
(True/False)
4.9/5  (44)
(44)
The additivity property of linear programming implies that the contribution of any decision variable to the objective is of/on the levels of the other decision variables.
(Multiple Choice)
4.8/5  (33)
(33)
In most cases in solving linear programming problems,we want the decision variables to be:
(Multiple Choice)
4.7/5  (41)
(41)
The prototype linear programming problem is to select an optimal mix of products to produce to maximize profit.This type of problem is referred to as the:
(Multiple Choice)
4.8/5  (36)
(36)
The proportionality property of LP models means that if the level of any activity is multiplied by a constant factor,then the contribution of this activity to the objective function,or to any of the constraints in which the activity is involved,is multiplied by the same factor.
(True/False)
4.7/5  (39)
(39)
What is the optimal shipping plan? What are the total costs in that case?
(Essay)
4.8/5  (40)
(40)
Suppose a company sells two different products,x and y,for net profits of $5 per unit and $10 per unit,respectively.The slope of the line representing the objective function is:
(Multiple Choice)
4.7/5  (27)
(27)
Consider the following linear programming problem: Maximize 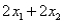 Subject to
Subject to 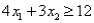
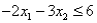
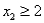
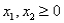 The above linear programming problem:
The above linear programming problem:
(Multiple Choice)
4.9/5  (23)
(23)
Showing 61 - 80 of 91
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)