Exam 31: Electromagnetic Oscillations and Alternating Current
Exam 1: Measurement31 Questions
Exam 2: Motion Along a Straight Line79 Questions
Exam 3: Vector39 Questions
Exam 4: Motion in Two and Three Dimensions47 Questions
Exam 5: Force and Motion I68 Questions
Exam 6: Force and Motion II71 Questions
Exam 7: Kinetic Energy and Work67 Questions
Exam 8: Potential Energy and Conservation of Energy61 Questions
Exam 9: Center of Mass and Linear Momentum81 Questions
Exam 10: Rotation82 Questions
Exam 11: Rolling, Torque, and Angular Momentum54 Questions
Exam 12: Equilibrium and Elasticity53 Questions
Exam 13: Gravitation55 Questions
Exam 14: Fluids85 Questions
Exam 15: Oscillations62 Questions
Exam 16: Waves I71 Questions
Exam 17: Waves II61 Questions
Exam 18: Temperature, Heat, and the First Law of Thermodynamics82 Questions
Exam 19: The Kinetic Theory of Gases95 Questions
Exam 20: Entropy and the Second Law of Thermodynamics56 Questions
Exam 21: Electric Charge45 Questions
Exam 22: Electric Fields49 Questions
Exam 23: Gauss Law34 Questions
Exam 24: Electric Potential44 Questions
Exam 25: Capacitance55 Questions
Exam 26: Current and Resistance49 Questions
Exam 27: Circuits70 Questions
Exam 28: Magnetic Fields48 Questions
Exam 29: Magnetic Fields Due to Currents47 Questions
Exam 30: Induction and Inductance85 Questions
Exam 31: Electromagnetic Oscillations and Alternating Current84 Questions
Exam 32: Maxwells Equations; Magnetism of Matter81 Questions
Exam 33: Electromagnetic Waves79 Questions
Exam 34: Images72 Questions
Exam 35: Interference40 Questions
Exam 36: Diffraction74 Questions
Exam 37: Relativity65 Questions
Exam 38: Photons and Matter Waves53 Questions
Exam 39: More About Matter Waves41 Questions
Exam 40: All About Atoms76 Questions
Exam 41: Conduction of Electricity in Solids48 Questions
Exam 42: Nuclear Physics67 Questions
Exam 43: Energy From the Nucleus44 Questions
Exam 44: Quarks, Leptons, and the Big Bang52 Questions
Select questions type
The total energy in an LC circuit is 5.0 *10-6 J. If L = 25 mH the maximum current is:
(Multiple Choice)
4.8/5  (36)
(36)
An RL series circuit is connected to an ac generator with a maximum emf of 20 V. If the maximum potential difference across the resistor is 16 V, then the maximum potential difference across the inductor is:
(Multiple Choice)
4.9/5  (38)
(38)
An LC circuit has a capacitance of 30 F and an inductance of 15 mH. At time t = 0 the charge on the capacitor is 10 C and the current is 20 mA. The maximum current is:
(Multiple Choice)
4.7/5  (32)
(32)
A 150-g block on the end of a spring with a spring constant of 35 N/m is pulled aside 25 cm and released from rest. In the electrical analog the initial charge on the capacitor is:
(Multiple Choice)
5.0/5  (32)
(32)
An ac generator producing 10 V (rms) at 200 rad/s is connected in series with a 50- resistor, a 400-mH inductor, and a 200- F capacitor. The rms current in amperes is:
(Multiple Choice)
4.9/5  (32)
(32)
A charged capacitor and an inductor are connected in series. At time t = 0 the current is zero, but the capacitor is charged. If T is the period of the resulting oscillations, the next time, after t = 0 that the energy stored in the magnetic field of the inductor is a maximum is:
(Multiple Choice)
4.8/5  (37)
(37)
The ideal meters shown read rms current and voltage. The average power delivered to the load is: 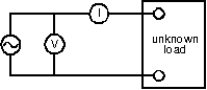
(Multiple Choice)
4.8/5  (26)
(26)
The average power supplied to the circuit shown passes through a maximum when which one of the following is increased continuously from a very low to a very high value? 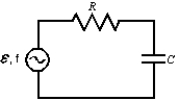
(Multiple Choice)
4.8/5  (46)
(46)
An ac generator producing 10 V (rms) at 200 rad/s is connected in series with a 50- resistor, a 400-mH inductor, and a 200- F capacitor. The rms voltage (in volts) across the resistor is:
(Multiple Choice)
4.7/5  (39)
(39)
An electric motor, under load, has an effective resistance of 30 and an inductive reactance of 40 . When powered by a source with a maximum voltage of 420 V, the maximum current is:
(Multiple Choice)
4.9/5  (37)
(37)
In an RLC series circuit, which is connected to a source of emf mcos( t), the current lags the voltage by 45 if:
(Multiple Choice)
4.9/5  (36)
(36)
A charged capacitor and an inductor are connected in series. At time t = 0 the current is zero, but the capacitor is charged. If T is the period of the resulting oscillations, the next time, after t = 0 that the charge on the capacitor is a maximum is:
(Multiple Choice)
4.9/5  (26)
(26)
The total energy in an LC circuit is 5.0 *10-6 J. If C = 15 F the charge on the capacitor is:
(Multiple Choice)
4.8/5  (34)
(34)
An LC series circuit with an inductance L and a capacitance C has an oscillation frequency f. Two inductors, each with inductance L, and two capacitors, each with capacitance C, are all wired in series and the circuit is completed. The oscillation frequency is:
(Multiple Choice)
4.8/5  (39)
(39)
At time t = 0 the charge on the 50- F capacitor in an LC circuit is 15 C and there is no current. If the inductance is 20 mH the maximum current is:
(Multiple Choice)
4.7/5  (34)
(34)
The rapid exponential decay in just a few cycles of the charge on the plates of capacitor in an RLC circuit might due to:
(Multiple Choice)
4.8/5  (32)
(32)
An LC circuit has an inductance of 20 mH and a capacitance of 5.0 F. At time t = 0 the charge on the capacitor is 3.0 F C and the current is 7.0 mA. The total energy is:
(Multiple Choice)
4.8/5  (38)
(38)
The rms value of a sinusoidal voltage is 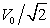 , where V0 is the amplitude. What is the rms value of its fully rectified wave? Recall that Vrect(t) = V(t) .
, where V0 is the amplitude. What is the rms value of its fully rectified wave? Recall that Vrect(t) = V(t) . 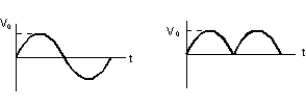
(Multiple Choice)
4.7/5  (26)
(26)
Showing 41 - 60 of 84
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)