Exam 11: Rolling, Torque, and Angular Momentum
Exam 1: Measurement31 Questions
Exam 2: Motion Along a Straight Line79 Questions
Exam 3: Vector39 Questions
Exam 4: Motion in Two and Three Dimensions47 Questions
Exam 5: Force and Motion I68 Questions
Exam 6: Force and Motion II71 Questions
Exam 7: Kinetic Energy and Work67 Questions
Exam 8: Potential Energy and Conservation of Energy61 Questions
Exam 9: Center of Mass and Linear Momentum81 Questions
Exam 10: Rotation82 Questions
Exam 11: Rolling, Torque, and Angular Momentum54 Questions
Exam 12: Equilibrium and Elasticity53 Questions
Exam 13: Gravitation55 Questions
Exam 14: Fluids85 Questions
Exam 15: Oscillations62 Questions
Exam 16: Waves I71 Questions
Exam 17: Waves II61 Questions
Exam 18: Temperature, Heat, and the First Law of Thermodynamics82 Questions
Exam 19: The Kinetic Theory of Gases95 Questions
Exam 20: Entropy and the Second Law of Thermodynamics56 Questions
Exam 21: Electric Charge45 Questions
Exam 22: Electric Fields49 Questions
Exam 23: Gauss Law34 Questions
Exam 24: Electric Potential44 Questions
Exam 25: Capacitance55 Questions
Exam 26: Current and Resistance49 Questions
Exam 27: Circuits70 Questions
Exam 28: Magnetic Fields48 Questions
Exam 29: Magnetic Fields Due to Currents47 Questions
Exam 30: Induction and Inductance85 Questions
Exam 31: Electromagnetic Oscillations and Alternating Current84 Questions
Exam 32: Maxwells Equations; Magnetism of Matter81 Questions
Exam 33: Electromagnetic Waves79 Questions
Exam 34: Images72 Questions
Exam 35: Interference40 Questions
Exam 36: Diffraction74 Questions
Exam 37: Relativity65 Questions
Exam 38: Photons and Matter Waves53 Questions
Exam 39: More About Matter Waves41 Questions
Exam 40: All About Atoms76 Questions
Exam 41: Conduction of Electricity in Solids48 Questions
Exam 42: Nuclear Physics67 Questions
Exam 43: Energy From the Nucleus44 Questions
Exam 44: Quarks, Leptons, and the Big Bang52 Questions
Select questions type
A cylinder of radius R = 6.0 cm is on a rough horizontal surface. The coefficient of kinetic friction between the cylinder and the surface is 0.30 and the rotational inertia for rotation about the axis is given by MR2/2, where M is its mass. Initially it is not rotating but its center of mass has a speed of 7.0 m/s. After 2.0 s the speed of its center of mass and its angular velocity about its center of mass, respectively, are:
(Multiple Choice)
4.8/5  (34)
(34)
A 2.0-kg block starts from rest on the positive x axis 3.0 m from the origin and thereafter has an acceleration given by 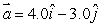 in m/s2. At the end of 2.0 s its angular momentum about the origin is:
in m/s2. At the end of 2.0 s its angular momentum about the origin is:
(Multiple Choice)
4.9/5  (30)
(30)
A man, with his arms at his sides, is spinning on a light frictionless turntable. When he extends his arms:
(Multiple Choice)
4.8/5  (33)
(33)
The angular momentum vector of Earth, due to its daily rotation, is directed:
(Multiple Choice)
4.9/5  (31)
(31)
A block with mass M, on the end of a string, moves in a circle on a horizontal frictionless table as shown. As the string is slowly pulled through a small hole in the table: 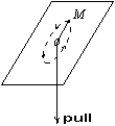
(Multiple Choice)
4.8/5  (44)
(44)
A 2.0-kg stone is tied to a 0.50-m long string and swung around a circle at a constant angular velocity of 12 rad/s. The net torque on the stone about the center of the circle is:
(Multiple Choice)
4.8/5  (37)
(37)
A wheel,with rotational inertia I, mounted on a vertical shaft with negligible ratational inertia, is rotating with angular speed 0. A nonrotation wheel with rotational inertia 2I is suddenly dropped onto the same shaft as shown.. The resultant combination of the two wheels and shaft will rotate at: 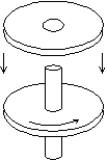
(Multiple Choice)
4.7/5  (33)
(33)
A wheel rolls without slipping along a horizontal road as shown. The velocity of the center of the wheel is represented by . Point P is painted on the rim of the wheel. The instantaneous velocity of point P is: 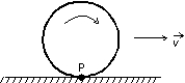
(Multiple Choice)
4.8/5  (31)
(31)
The coefficient of static friction between a certain cylinder and a horizontal floor is 0.40. If the rotational inertia of the cylinder about its symmetry axis is given by I = (1/2)MR2, then the maximum acceleration the cylinder can have without sliding is:
(Multiple Choice)
4.9/5  (42)
(42)
As a 2.0-kg block travels around a 0.50-m radius circle it has an angular speed of 12 rad/s. The circle is parallel to the xy plane and is centered on the z axis, 0.75 m from the origin. The magnitude of its angular momentum around the origin is:
(Multiple Choice)
4.8/5  (38)
(38)
A playground merry-go-round has a radius R and a rotational inertia I. When the merry-go-round is at rest, a child with mass m runs with speed v along a line tangent to the rim and jumps on. The angular velocity of the merry-go-round is then:
(Multiple Choice)
4.7/5  (42)
(42)
A playground merry-go-round has a radius of 3.0 m and a rotational inertia of 600 kg .m2. It is initially spinning at 0.80 rad/s when a 20-kg child crawls from the center to the rim. When the child reaches the rim the angular velocity of the merry-go-round is:
(Multiple Choice)
4.9/5  (26)
(26)
A solid wheel with mass M, radius R, and rotational inertia MR2/2, rolls without sliding on a horizontial surface. A horizontal force F is applied to the axle and the center of mass has an acceleration a. The magnitudes of the applied force F and the frictional force f of the surface, respectively, are:
(Multiple Choice)
5.0/5  (31)
(31)
A wheel of radius 0.5 m rolls without sliding on a horizontal surface as shown. Starting from rest, the wheel moves with constant angular acceleration 6 rad/s2. The distance in traveled by the center of the wheel from t = 0 to t = 3 s is: 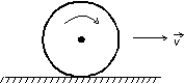
(Multiple Choice)
4.8/5  (36)
(36)
A particle, held by a string whose other end is attached to a fixed point C, moves in a circle on a horizontal frictionless surface. If the string is cut, the angular momentum of the particle about the point C:
(Multiple Choice)
4.8/5  (29)
(29)
Two objects are moving in the x,,y plane as shown. The magnitude of their total angular momentum (about the origin O) is: 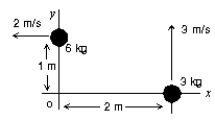
(Multiple Choice)
4.8/5  (27)
(27)
A man, holding a weight in each hand, stands at the center of a horizontal frictionless rotating turntable. The effect of the weights is to double the rotational inertia of the system. As he is rotating, the man opens his hands and drops the two weights. They fall outside the turntable. Then:
(Multiple Choice)
4.8/5  (32)
(32)
A 15-g paper clip is attached to the rim of a phonograph record with a radius of 30 cm, spinning at 3.5 rad/s. The magnitude of its angular momentum is:
(Multiple Choice)
4.8/5  (35)
(35)
A 6.0-kg particle moves to the right at 4.0 m/s as shown. The magnitude of its angular momentum about the point O is: 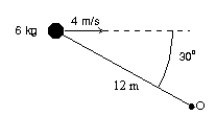
(Multiple Choice)
4.9/5  (32)
(32)
Showing 21 - 40 of 54
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)