Exam 16: Waves I
Exam 1: Measurement37 Questions
Exam 2: Motion Along a Straight Line90 Questions
Exam 3: Vector37 Questions
Exam 4: Motion in Two and Three Dimensions56 Questions
Exam 5: Force and Motion I73 Questions
Exam 6: Force and Motion II74 Questions
Exam 7: Kinetic Energy and Work73 Questions
Exam 8: Potential Energy and Conservation of Energy63 Questions
Exam 9: Center of Mass and Linear Momentum99 Questions
Exam 10: Rotation102 Questions
Exam 11: Rolling, Torque, and Angular Momentum66 Questions
Exam 12: Equilibrium and Elasticity57 Questions
Exam 13: Gravitation55 Questions
Exam 14: Fluids88 Questions
Exam 15: Oscillations75 Questions
Exam 16: Waves I82 Questions
Exam 17: Waves II71 Questions
Exam 18: Temperature, Heat, and the First Law of Thermodynamics96 Questions
Exam 19: The Kinetic Theory of Gases113 Questions
Exam 20: Entropy and the Second Law of Thermodynamics61 Questions
Exam 21: Electric Charge52 Questions
Exam 22: Electric Fields55 Questions
Exam 23: Gauss Law38 Questions
Exam 24: Electric Potential52 Questions
Exam 25: Capacitance61 Questions
Exam 26: Current and Resistance55 Questions
Exam 27: Circuits73 Questions
Exam 28: Magnetic Fields55 Questions
Exam 29: Magnetic Fields Due to Currents49 Questions
Exam 30: Induction and Inductance90 Questions
Exam 31: Electromagnetic Oscillations and Alternating Current88 Questions
Exam 32: Maxwells Equations; Magnetism of Matter81 Questions
Exam 33: Electromagnetic Waves83 Questions
Exam 34: Images79 Questions
Exam 35: Interference46 Questions
Exam 36: Diffraction77 Questions
Exam 37: Relativity68 Questions
Exam 38: Photons and Matter Waves57 Questions
Exam 39: More About Matter Waves41 Questions
Exam 40: All About Atoms79 Questions
Exam 41: Conduction of Electricity in Solids51 Questions
Exam 42: Nuclear Physics68 Questions
Exam 43: Energy From the Nucleus50 Questions
Exam 44: Quarks, Leptons, and the Big Bang55 Questions
Select questions type
A 30-cm long string, with one end clamped and the other free to move transversely, is vibrating in its second harmonic. The wavelength of the constituent traveling waves is:
Free
(Multiple Choice)
4.8/5  (40)
(40)
Correct Answer:
C
A wave is described by y(x,t) = 0.1 sin(3x + 10t), where x is in meters, y is in centimeters and t is in seconds. The angular wave number is:
Free
(Multiple Choice)
4.7/5  (32)
(32)
Correct Answer:
E
A transverse wave travels on a string of length 1.3 m and diameter 1.1 mm, whose mass is 10 g and which is under a tension of 16 N. What is the linear mass density of the string?
Free
(Multiple Choice)
4.9/5  (32)
(32)
Correct Answer:
A
Let f be the frequency, v the speed, and T the period of a sinusoidal traveling wave. The correct relationship is:
(Multiple Choice)
4.8/5  (28)
(28)
A sinusoidal wave is generated by moving the end of a string up and down periodically. The generator does not supply any power when the end of the string
(Multiple Choice)
4.8/5  (40)
(40)
A standing wave pattern is established in a string as shown. The wavelength of one of the component traveling waves is: 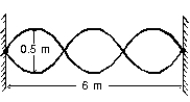
(Multiple Choice)
4.9/5  (36)
(36)
When a string is vibrating in a standing wave pattern the power transmitted across an antinode, compared to the power transmitted across a node, is:
(Multiple Choice)
4.8/5  (33)
(33)
The displacement of an element of a string is given by y(x,t) = 4.3sin(1.2x - 4.7t - π/3), with x in meters and t in seconds. Given that , what is v?
(Multiple Choice)
4.8/5  (41)
(41)
A long string is constructed by joining the ends of two shorter strings. The tension in the strings is the same but string I has 4 times the linear mass density of string II. When a sinusoidal wave passes from string I to string II:
(Multiple Choice)
4.9/5  (33)
(33)
When a certain string is clamped at both ends, the lowest four resonant frequencies are measured to be 100, 150, 200, and 250 Hz. One of the resonant frequencies (below 200 Hz) is missing. What is it?
(Multiple Choice)
4.7/5  (31)
(31)
The tension in a string with a linear density of 0.0010 kg/m is 0.40 N. A 100 Hz sinusoidal wave on this string has a wavelength of:
(Multiple Choice)
4.8/5  (36)
(36)
The displacement of a string carrying a traveling sinusoidal wave is given by 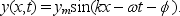 At time t = 0 the point at x = 0 has velocity v0 and displacement y0. The phase constant is given by tan =:
At time t = 0 the point at x = 0 has velocity v0 and displacement y0. The phase constant is given by tan =:
(Multiple Choice)
4.9/5  (37)
(37)
A string of length 100 cm is held fixed at both ends and vibrates in a standing wave pattern. The wavelengths of the constituent traveling waves CANNOT be:
(Multiple Choice)
4.9/5  (34)
(34)
Two waves are traveling on two different strings. The displacement of one is given by y1(x,t) = ymsin(kx + t) and of the other by y2(x,t) = ymsin(kx + t + φ). What is the difference between these two waves?
(Multiple Choice)
4.9/5  (36)
(36)
The sinusoidal wave y(x,t) = ymsin(kx - t)
Is incident on the fixed end of a string at x = L. The reflected wave is given by:
(Multiple Choice)
4.8/5  (28)
(28)
A traveling sinusoidal wave is shown below. At which point is the motion 180 out of phase with the motion at point P? 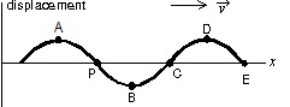
(Multiple Choice)
4.7/5  (36)
(36)
A 40-cm long string, with one end clamped and the other free to move transversely, is vibrating in its fundamental standing wave mode. The wavelength of the constituent traveling waves is:
(Multiple Choice)
4.8/5  (32)
(32)
The sum of two sinusoidal traveling waves is a sinusoidal traveling wave only if:
(Multiple Choice)
4.7/5  (40)
(40)
Showing 1 - 20 of 82
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)