The Following Graph Shows the Actual Percentage of U $P ( x ) = \frac { 93 } { 1 + 5.35 ( 1.05 ) ^ { - x } }$

Multiple Choice

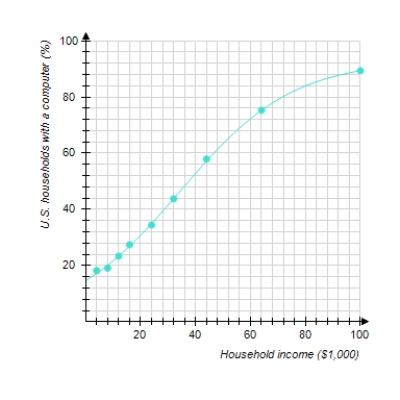
The following graph shows the actual percentage of U.S. households with a computer as a function of household income (the data points) and a logistic model of these data (the curve) . The logistic model is
$P ( x ) = \frac { 93 } { 1 + 5.35 ( 1.05 ) ^ { - x } }$
Where x is the household income in thousands of dollars. For low incomes, the logistic model is approximately exponential. Which exponential model best approximates P(x) for small x Round the coefficients to the nearest hundredth.

A) $P ( x ) = 17.65 ( 2.1 ) ^ { x }$
B) $P ( x ) = 14.65 ( 1.05 ) ^ { - x }$
C) $P ( x ) = 17.65 ( 1.05 ) ^ { x }$
D) $P ( x ) = 14.65 ( 1.05 ) ^ { x }$
E) $P ( x ) = 14.65 ( 2.1 ) ^ { - x }$