An Article Describes the Results of an Experiment

Multiple Choice

An article describes the results of an experiment. Patients suffering from chronic somatic diseases were randomly assigned to the two groups. One group was a control group of patients who received treatment A. Of the 58 patients in this group, 9 reported improvements at the end of the study period. Patients in the second group received treatment B. Of the 33 patients in this group, 4 reported improvements at the end of the study period. ​
Do these data provide evidence that the proportion of success for patients who received treatment A differs from the proportion of success for patients who received treatment B? Use a randomization test to select the appropriate output for one set of 1000 simulated proportions and carry out a hypothesis test for a difference in proportions. Use a significance level of 0.05.
​

A)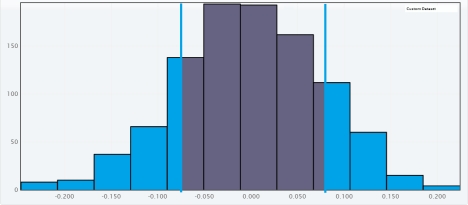
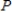​ ​The approximate -value is 0.316.Since it is lower than 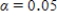, we reject 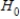for a significance level of 0.05 .There is significant difference between the proportion of success for patients who received treatment A and the proportion of success for patients who received treatment B.
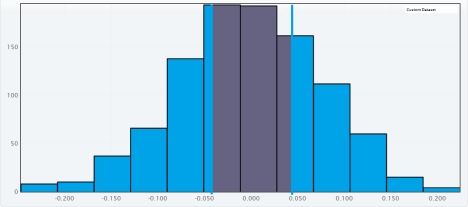
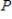B) ​ ​The approximate -value is 0.655.Since it is greater than 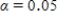, we fail to reject 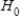for a significance level of 0.05.There is not convincing evidence that there is difference between the proportion of success for patients who received treatment A and the proportion of success for patients who received treatment B.​
C) ​ ​
The approximate 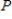-value is 0.345.Since it is greater than 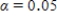, we reject 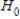for a significance level of 0.05.There is significant difference between the proportion of success fot patients who received treatment A and the proportion of success for patients who received treatment B.
D) ​ ​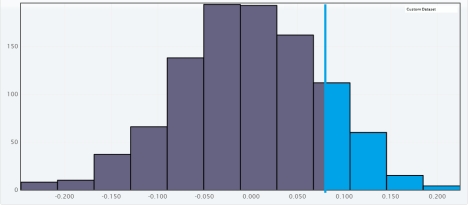
The approximate 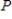-value is 0.034.Since it is lower than 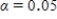, we reject for a significance level of 0.05.There is significant difference between the proportion of success for patients who received treatment A and the proportion of success for patients who received treatment B.
E) ​ ​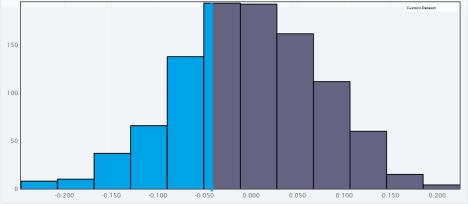
The approximate 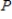-value is 0.966.Since it is greater than , we reject for a significance level of 0.05 .There is not convincing evidence that there is difference between the proportion of success for patients who received treatment A and the proportion of success for patients who received treatment B.​