Multiple Choice
Sketch the graph of the equation. If the graph is a parabola, find its vertex. If the graph is a circle, find its center andradius.

A) 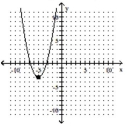
B) 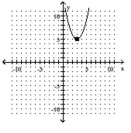
C) 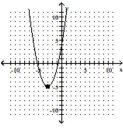
D) 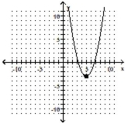
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q69: Solve.<br>-A rectangular holding pen for sheep
Q70: The graph of the equation is
Q71: The graph of the equation is
Q72: Find the center and the radius
Q73: Graph the equation.<br>- <span class="ql-formula" data-value="x
Q75: Sketch the graph of the equation.
Q76: Find the center and the radius
Q77: Graph the system.<br>- <span class="ql-formula" data-value="\left\{
Q78: Graph the system.<br>- <span class="ql-formula" data-value="\left\{
Q79: Fill in the blank with one