Related Questions
Q49: Provide an appropriate response.<br>- <span class="ql-formula"
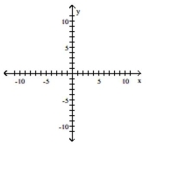
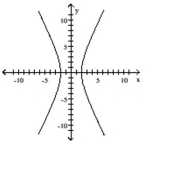
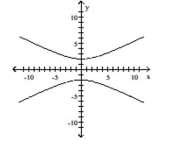
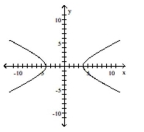
Q50: Graph the hyperbola.<br>- <span class="ql-formula" data-value="\frac
Q51: Provide an appropriate response.<br>- <span class="ql-formula"
Q52: Graph the conic section.<br>- <span class="ql-formula"
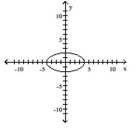
Q53: Match the equation of the ellipse
Q55: Write an equation for the parabola.<br>-vertex
Q56: Find the center, foci, and asymptotes
Q57: Find the center, foci, and asymptotes
Q58: Match the equation of the parabola
Q59: Write an equation for the ellipse.<br>-