Discuss the Equation and Graph It A)directrix Perpendicular to Polar Axis 8 Right of Pole
Center
Multiple Choice
Discuss the equation and graph it.
- 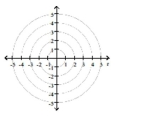
A) directrix perpendicular to polar axis 8 right of pole
center
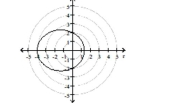
B) directrix parallel to polar axis 8 above pole center
vertices 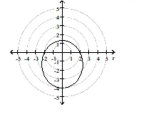
C) directrix perpendicular to polar axis 8 left of pole
center
vertices 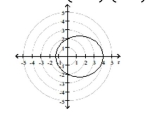
D) directrix parallel to polar axis 8 below pole center
vertices 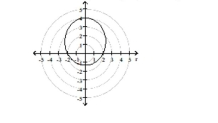
Correct Answer:

Verified
Correct Answer:
Verified
Q121: Find an equation for the ellipse
Q122: Identify the equation without completing the
Q123: Solve the problem.<br>-A bridge is built in
Q124: Find the vertex, focus, and directrix
Q125: Find an equation for the hyperbola
Q127: Find an equation of the parabola
Q128: Find the vertex, focus, and directrix
Q129: Graph the ellipse and locate the
Q130: Graph the hyperbola.<br>- <span class="ql-formula" data-value="\frac{y^{2}}{4}-\frac{x^{2}}{16}=1"><span
Q131: Rotate the axes so that the