Students a Growing School District Tracks the Student Population Growth $= 119.53 + 172.03$

Essay

Students A growing school district tracks the student population growth over the years
from 2008 to 2013. Here are the regression results and a residual plot. students $= 119.53 + 172.03$ year
Sample size: 6
$\mathrm { R } - \mathrm { sq } = 0.987$
students $= 119.53 + 172.03$ y
Sample size: 6
R-sq 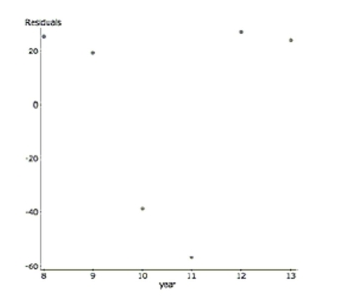$= 0.987$



a. Explain why despite a high R-sq, this regression is not a successful model.
To linearize the data, the log (base 10) was taken of the student population. Here are the results.
Dependent Variable: log(students) Sample size: 6
$$\mathrm { R } - \mathrm { sq } = 0.994$$
$\begin{array} { l r r } \text { Parameter } & \text { Estimate } & \text { Std. Err. } \\ \text { constant } & 2.871 & 0.0162 \\ \text { year } & 0.0389 & 0.00152 \end{array}$



b. Describe the success of the linearization.
c. Interpret R-sq in the context of this problem.
d. Predict the student population in 2014.