Solve the Problem $\theta$ To an Observer, Where $\theta = \tan ^ { - 1 } \left( \frac { x } { x ^ { 2 } + 1.6 } \right)$

Multiple Choice

Solve the problem.
-A painting 1 meter high and 3 meters from the floor will cut off an angle $\theta$ to an observer, where $\theta = \tan ^ { - 1 } \left( \frac { x } { x ^ { 2 } + 1.6 } \right)$ , assuming that the observer is $x$ feet from the wall where the painting is displayed and that the eyes of the observer are $1.6$ meters above the ground (see the figure) . Find the value of $\theta$ for $x = 3$ . Round to the nearest tenth of a degree.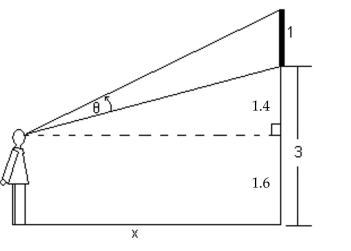

A) $13.3 ^ { \circ }$
B) $18.3 ^ { \circ }$
C) $15.8 ^ { \circ }$
D) $33.1 ^ { \circ }$