Multiple Choice
Graph the equation. Include the coordinates of any local and absolute extreme points and inflection points.
- 
A)
local minimum:
local maximum:
inflection point: 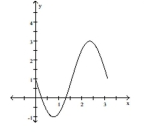
B)
local minimum:
local maximum:
inflection points: 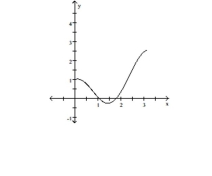
C) C) no local extrema
inflection point: 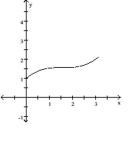
D) local minimum:
local maximum:
inflection points: 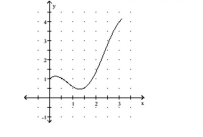
Correct Answer:

Verified
Correct Answer:
Verified
Q299: Graph the equation. Include the coordinates
Q300: Answer each question appropriately.<br>-Suppose the velocity
Q301: Graph the equation. Include the coordinates
Q302: Use l'Hopital's Rule to evaluate the
Q303: Solve the problem.<br>-The graph below shows
Q305: Graph the equation. Include the coordinates
Q306: Estimate the limit by graphing the
Q307: Find the most general antiderivative.<br>- <span
Q308: Determine from the graph whether the function
Q309: Sketch the graph and show all