Solve Applied Problems Involving Hyperbolas
Solve the Problem $( 0,3 )$

Multiple Choice

Solve Applied Problems Involving Hyperbolas
Solve the problem.
-A satellite following the hyperbolic path shown in the picture turns rapidly at $( 0,3 )$ and then moves closer and closer to the line $\mathrm { y } = \frac { 5 } { 2 } \mathrm { x }$ as it gets farther from the tracking station at the origin. Find the equation that describes the path of the satellite if the center of the hyperbola is at 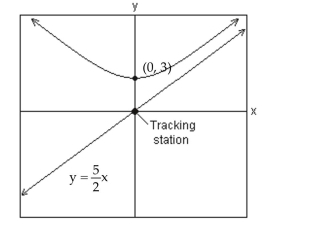$( 0,0 )$ .

A) $\frac { y ^ { 2 } } { 9 } - \frac { x ^ { 2 } } { \frac { 36 } { 25 } } = 1$
B) $\frac { x ^ { 2 } } { 9 } - \frac { y ^ { 2 } } { \left( \frac { 75 } { 6 } \right) ^ { 2 } } = 1$
C) $\frac { y ^ { 2 } } { \frac { 36 } { 25 } } - \frac { x ^ { 2 } } { 9 } = 1$
D) $\frac { x ^ { 2 } } { \left( \frac { 75 } { 6 } \right) ^ { 2 } } - \frac { y ^ { 2 } } { 9 } = 1$