Multiple Choice
Solve Problems Involving Systems Without Unique Solutions
Solve the problem using matrices.
-The figure below shows the intersection of three one-way streets. To keep traffic moving, the number of cars per minute entering an intersection must equal the number of cars leaving that intersection. Set up a
System of equations that keeps traffic moving, and use Gaussian elimination to solve the system. If
Construction limits z to t cars per minute, how many cars per minute must pass through the other
Intersections to keep traffic moving? 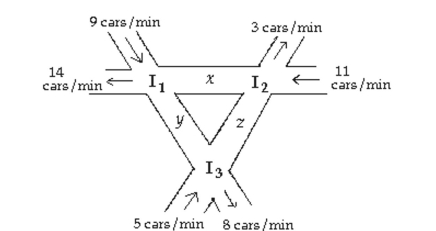
A) cars between and between and
B) cars between and between and
C) cars between and cars/min between and
D) cars between and between and
Correct Answer:

Verified
Correct Answer:
Verified
Q123: Find the products AB and BA
Q124: Solve the problem.<br>-Let <span class="ql-formula"
Q125: Understand What is Meant by Equal
Q126: Solve the problem using matrices.<br>-State University has
Q127: Encode and Decode Messages<br>Encode or decode
Q129: Apply Gaussian Elimination to Systems Without
Q130: Solve the problem.<br>-Let <span class="ql-formula"
Q131: Solve the problem.<br>- <span class="ql-formula" data-value="\left|
Q132: Use Cramer's rule to solve the
Q133: Encode and Decode Messages<br>Encode or decode