Essay

-Supply missing statements and missing reasons for the following proof.
Given: 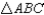 ;
; 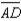 bisects
bisects 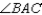 and
and 
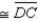 Prove:
Prove: 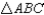 is an isosceles triangle
is an isosceles triangle
S1. 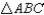 ;
; 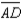 bisects
bisects 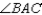 R1.
R1.
S2. 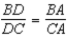 R2. If a ray bisects one
R2. If a ray bisects one 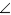 of a
of a  , it divides the opposite
, it divides the opposite
side into segments whose lengths are proportional to
the lengths of the two sides that form the bisected 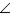 .
.
S3. R3. Given
S4. 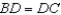 R4.
R4.
S5. 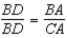 , so
, so 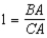 R5.
R5.
S6. 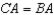 R6.
R6.
S7. R7.
Correct Answer:

Verified
R1. Given
S3. 
 R4. Definition of congru...
R4. Definition of congru...View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Correct Answer:
Verified
S3.
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q2: Where <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt="Where and
Q3: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Supply missing statements
Q4: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Supply the missing
Q5: Explain (prove) the following property of proportions.<br>"If
Q6: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Supply missing statements
Q7: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Provide all statements
Q8: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Use the drawing
Q9: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Use the drawing(s)
Q10: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Provide the missing
Q12: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7237/.jpg" alt=" -Supply missing statements