Multiple Choice
Analyze and sketch a graph of the function
A) 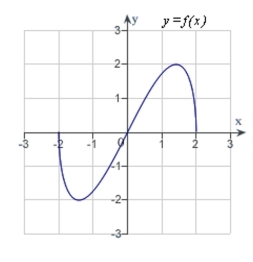
B) 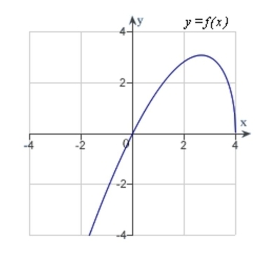
C) 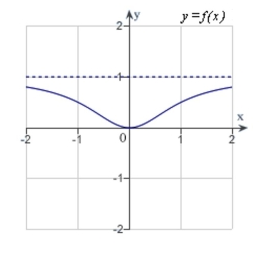
D) 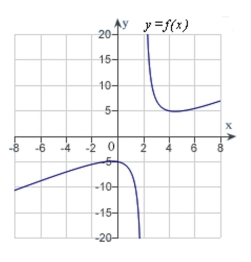
E) 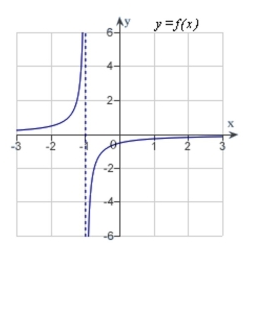
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q107: The resistance R of a certain
Q108: <span class="ql-formula" data-value="\text { Determine the open
Q109: Locate the absolute extrema of the
Q110: Determine whether the Mean Value Theorem
Q111: A meteorologist measures the atmospheric pressure
Q113: Analyze the graph of the function
Q114: A company introduces a new product
Q115: <span class="ql-formula" data-value="\text { Find the relative
Q116: <span class="ql-formula" data-value="\text { Find all critical
Q117: Find the relative minima of