Solved

Find the Area of the Shaded Region y=14exy = \frac { 1 } { 4 } e ^ { x }

Question 84

Multiple Choice

Find the area of the shaded region. 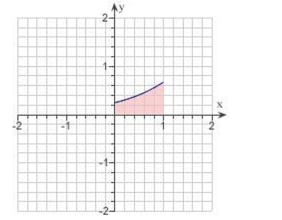y=14exy = \frac { 1 } { 4 } e ^ { x } Find the area of the shaded region. y = \frac { 1 } { 4 } e ^ { x } A) \frac { 1 } { 4 } B) 4 e C) 1 D) \frac { e } { 4 } E) \frac { e - 1 } { 4 }


A) 14\frac { 1 } { 4 }
B) 4e4 e
C) 1
D) e4\frac { e } { 4 }
E) e−14\frac { e - 1 } { 4 }

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q79: Use the summation formulas to rewrite

Q80: Evaluate the integral. <span class="ql-formula"

Q81: Evaluate the following definite integral.

Q82: Apply the Trapezoidal Rule and Simpson's

Q83: Use the Trapezoidal Rule to approximate

Q85: <span class="ql-formula" data-value="\text { Use the differential

Q86: <span class="ql-formula" data-value="\text { Use integration to

Q87: Evaluate the definite integral of the

Q88: <span class="ql-formula" data-value="\text { Find } F

Q89: Use the properties of summation and