Determine the Location of the Horizontal Axis $y _ { a } \text { for figure (b) at which a vertical }$

Multiple Choice

Determine the location of the horizontal axis $y _ { a } \text { for figure (b) at which a vertical }$ gate in a dam is to be hinged so that there is no moment causing rotation under the indicated loading (see figure (a) ) . The model for $y _ { a }$ is $y _ { a } = \bar { y } - \frac { I _ { \bar { y } } } { h A }$ where $\bar { y }$ is the $y$ -coordinate of the centroid of the gate, $L _ { y }$ is the moment of inertia of the gate about the line $y = \bar { y } , h$ is the depth of the centroid below the surface, and $A$ is the area of the gate.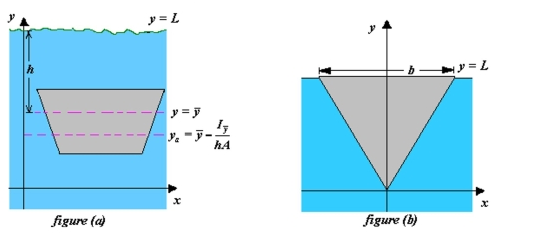

A) $y _ { a } = \frac { a ( 3 L - 2 a ) } { 2 ( 3 L + a ) }$
B) $y _ { a } = \frac { 2 L } { 3 }$
C) $y _ { a } = \frac { L } { 3 }$
D) $y _ { a } = \frac { L } { 2 }$
E) $y _ { a } = \frac { a ( 2 L + 3 a ) } { 3 ( 3 L - a ) }$