Multiple Choice
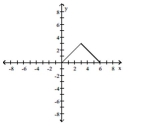
Find a formula for the function graphed.
-
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q91: Determine if the function is even,
Q92: Find a formula for the function
Q93: Find the formula for the function.<br>-Express
Q94: Find the domain and range of
Q95: Graph the function. Determine the symmetry,
Q97: Find the domain and range for
Q98: Find a formula for the function
Q99: Graph the function. Specify the intervals
Q100: Provide an appropriate response.<br>- <span class="ql-formula"
Q101: Find the domain and graph the