Multiple Choice
Find the extrema of the function by analyzing its graph below. 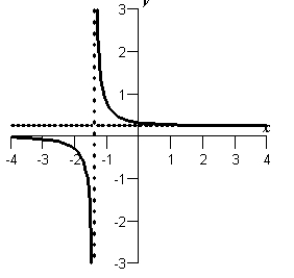
A) (0, 1)
B) no relative extrema
C) , (0, 0)
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q76: Find the equation of the tangent
Q77: Find <span class="ql-formula" data-value="f ^
Q78: Evaluate the expression <span class="ql-formula"
Q79: Sketch the graph of the function
Q80: Find <span class="ql-formula" data-value="y ^
Q82: Solve the following equation for
Q83: Write the expression <span class="ql-formula"
Q84: Use the properties of exponents to
Q85: If <span class="ql-formula" data-value="4 x
Q86: A survey of high school seniors