Solved

Graph the Curve Described by the Function, Indicating the Positive ≤\le

Question 60

Multiple Choice

Graph the curve described by the function, indicating the positive orientation.
-r(t) = 2cos t i + 3j + 2 sin t k, for 0 ≤\le t ≤\le 2 π\pi


A)
Graph the curve described by the function, indicating the positive orientation. -r(t) = 2cos t i + 3j + 2 sin t k, for 0 \le t \le 2 \pi A) B) C) D)
B)
Graph the curve described by the function, indicating the positive orientation. -r(t) = 2cos t i + 3j + 2 sin t k, for 0 \le t \le 2 \pi A) B) C) D)
C)
Graph the curve described by the function, indicating the positive orientation. -r(t) = 2cos t i + 3j + 2 sin t k, for 0 \le t \le 2 \pi A) B) C) D)
D)
Graph the curve described by the function, indicating the positive orientation. -r(t) = 2cos t i + 3j + 2 sin t k, for 0 \le t \le 2 \pi A) 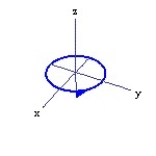B) C) 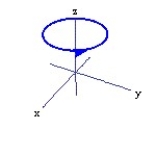D)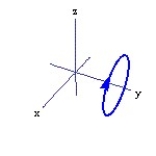

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q55: Find the unit tangent vector T and

Q56: Find the unit tangent vector T

Q57: Find the unit tangent vector of the

Q58: Evaluate the integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the integral.

Q59: If r(t) is the position vector of

Q61: Find the curvature of the curve r(t).<br>-r(t)

Q62: Evaluate the integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the integral.

Q63: Evaluate the integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the integral.

Q64: FInd the tangential and normal components of

Q65: Compute r''(t).<br>-r(t) = ( 3 ln( 6t))i