Solved

Find the Unit Tangent Vector of the Given Curve

Question 57

Multiple Choice

Find the unit tangent vector of the given curve.
-r(t) = ( 8t cos t - 8 sin t) j + ( 8t sin t + 8 cos t) k


A) T = (-8 sin t) j + ( 8 cos t) k
B) T = ( 8 cos t) j - ( 8 sin t) k
C) T = (-sin t) j + (cos t) k
D) T = - Find the unit tangent vector of the given curve. -r(t) = ( 8t cos t - 8 sin t) j + ( 8t sin t + 8 cos t) k A) T = (-8 sin t) j + ( 8 cos t) k B) T = ( 8 cos t) j - ( 8 sin t) k C) T = (-sin t) j + (cos t) k D) T = - (sin t) j + (cos t) k (sin t) j + Find the unit tangent vector of the given curve. -r(t) = ( 8t cos t - 8 sin t) j + ( 8t sin t + 8 cos t) k A) T = (-8 sin t) j + ( 8 cos t) k B) T = ( 8 cos t) j - ( 8 sin t) k C) T = (-sin t) j + (cos t) k D) T = - 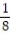(sin t) j + 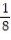(cos t) k (cos t) k

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q52: FInd the tangential and normal components of

Q53: Verify that the curve r(t) lies on

Q54: Find the curvature of the space curve.<br>-r(t)

Q55: Find the unit tangent vector T and

Q56: Find the unit tangent vector T

Q58: Evaluate the integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the integral.

Q59: If r(t) is the position vector of

Q60: Graph the curve described by the

Q61: Find the curvature of the curve r(t).<br>-r(t)

Q62: Evaluate the integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the integral.