Solved

Find the Curvature of the Space Curve

Question 54

Multiple Choice

Find the curvature of the space curve.
-r(t) = ti + (sinh t) j + (cosh t) k


A) 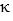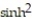Find the curvature of the space curve. -r(t) = ti + (sinh t) j + (cosh t) k A) = t B) = C) = t D) = = Find the curvature of the space curve. -r(t) = ti + (sinh t) j + (cosh t) k A) = t B) = C) = t D) = t
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = 11ee9522_3543_65b3_bdb6_91869b3538ab_TB9662_11
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = 11ee9522_3543_8cc4_bdb6_250adba12ef6_TB9662_11 t
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = 11ee9522_3543_8cc5_bdb6_071c3343abdb_TB9662_11

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q49: Find the domain of the vector-valued

Q50: The position vector of a particle is

Q51: If r(t) is the position vector of

Q52: FInd the tangential and normal components of

Q53: Verify that the curve r(t) lies on

Q55: Find the unit tangent vector T and

Q56: Find the unit tangent vector T

Q57: Find the unit tangent vector of the

Q58: Evaluate the integral.<br>-<img src="https://d2lvgg3v3hfg70.cloudfront.net/TB9662/.jpg" alt="Evaluate the integral.

Q59: If r(t) is the position vector of