Multiple Choice
Consider the first-order homogeneous system of linear differential equations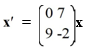
Which of these is the general solution of the system? Here, C1 and C2 are arbitrary real constants.
A)
B)
C)
D)
E)
Correct Answer:

Verified
Correct Answer:
Verified
Q71: Consider the first-order nonhomogeneous initial value
Q72: Consider the matrix function<br>A(t) = <img
Q73: Consider the first-order homogeneous system of
Q74: Consider the first-order homogeneous system of linear
Q75: Consider the first-order homogeneous system of
Q77: Consider the first-order homogeneous system of
Q78: Suppose Tank A contains 50 gallons of
Q79: Consider the first-order homogeneous system of linear
Q80: Consider the first-order homogeneous system of
Q81: Consider the first-order homogeneous system of linear