Multiple Choice
Consider the first-order nonhomogeneous initial value problem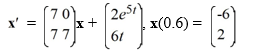
Given a fundamental matrix 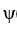 (t) for the system, what is the solution of this initial value problem?
(t) for the system, what is the solution of this initial value problem?
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Q66: Consider the first-order homogeneous system of linear
Q67: Consider the first-order homogeneous system of
Q68: Into which of the following systems can
Q69: Consider the first-order homogeneous system of linear
Q70: Consider the matrix function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q72: Consider the matrix function<br>A(t) = <img
Q73: Consider the first-order homogeneous system of
Q74: Consider the first-order homogeneous system of linear
Q75: Consider the first-order homogeneous system of
Q76: Consider the first-order homogeneous system of