Solved

Consider the First-Order Homogeneous System of Linear Differential Equations
x(t)=C1(3−10)e−2t+C2(01)e−5t \mathbf{x}(t)=C_{1}\left(\begin{array}{l}3 \\ -10\end{array}\right) e^{-2 t}+C_{2}\left(\begin{array}{l}0 \\ 1\end{array}\right) e^{-5 t}

Question 8

Multiple Choice

Consider the first-order homogeneous system of linear differential equations
Consider the first-order homogeneous system of linear differential equations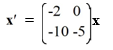 Which of these is the general solution of the system? Here, C<sub>1</sub> and C<sub>2</sub> are arbitrary real constants. A) \mathbf{x}(t) =C_{1}\left(\begin{array}{l}3 \\ -10\end{array}\right) e^{-2 t}+C_{2}\left(\begin{array}{l}0 \\ 1\end{array}\right) e^{-5 t} B) \mathbf{x}(t) =C_{1}\left(\begin{array}{l}3 \\ -10\end{array}\right) e^{-2 t}+C_{2}\left(\begin{array}{c}0 \\ -1\end{array}\right) e^{5 t} C) \mathbf{x}(t) =C_{1}\left(\begin{array}{l}3 \\ -10\end{array}\right) e^{-2 t}+C_{2}\left(\begin{array}{l}-10 \\ -3\end{array}\right) e^{2 t} D) \mathbf{x}(t) =C_{1}\left(\begin{array}{l}-1 \\ 0\end{array}\right) e^{5 t}+C_{2}\left(\begin{array}{l}3 \\ -10\end{array}\right) e^{-2 t} E) \mathbf{x}(t) =C_{1}\left(\begin{array}{l}0 \\ 1\end{array}\right) e^{-5 t}+C_{2}\left(\begin{array}{l}-10 \\ -3\end{array}\right) e^{2 t}
Which of these is the general solution of the system? Here, C1 and C2 are arbitrary real constants.


A) x(t) =C1(3−10) e−2t+C2(01) e−5t \mathbf{x}(t) =C_{1}\left(\begin{array}{l}3 \\ -10\end{array}\right) e^{-2 t}+C_{2}\left(\begin{array}{l}0 \\ 1\end{array}\right) e^{-5 t}
B) x(t) =C1(3−10) e−2t+C2(0−1) e5t \mathbf{x}(t) =C_{1}\left(\begin{array}{l}3 \\ -10\end{array}\right) e^{-2 t}+C_{2}\left(\begin{array}{c}0 \\ -1\end{array}\right) e^{5 t}
C) x(t) =C1(3−10) e−2t+C2(−10−3) e2t \mathbf{x}(t) =C_{1}\left(\begin{array}{l}3 \\ -10\end{array}\right) e^{-2 t}+C_{2}\left(\begin{array}{l}-10 \\ -3\end{array}\right) e^{2 t}
D) x(t) =C1(−10) e5t+C2(3−10) e−2t \mathbf{x}(t) =C_{1}\left(\begin{array}{l}-1 \\ 0\end{array}\right) e^{5 t}+C_{2}\left(\begin{array}{l}3 \\ -10\end{array}\right) e^{-2 t}
E) x(t) =C1(01) e−5t+C2(−10−3) e2t \mathbf{x}(t) =C_{1}\left(\begin{array}{l}0 \\ 1\end{array}\right) e^{-5 t}+C_{2}\left(\begin{array}{l}-10 \\ -3\end{array}\right) e^{2 t}

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q3: Consider this system of first-order differential equations:<br>

Q4: Consider the first-order homogeneous system of linear

Q5: Consider the first-order homogeneous system of

Q6: Transform this nonhomogeneous second-order initial value problem

Q7: Consider the first-order homogeneous system of linear

Q9: Consider the first-order homogeneous system of

Q10: Consider the first-order homogeneous system of

Q11: Consider the first-order homogeneous system of

Q12: Consider the first-order homogeneous system of

Q13: Consider the first-order homogeneous system of linear