Consider the First-Order Homogeneous System of Linear Differential Equations
$\rightarrow$

Multiple Choice

Consider the first-order homogeneous system of linear differential equations

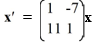
Determine the eigenvalues for this system and describe the behavior of the solution trajectories as t $\rightarrow$$\infty$ .

A) $\lambda=1 \pm i \sqrt{77}$ ; all solution trajectories spiral toward the origin as $t \rightarrow \infty$ .
B) $\lambda=1 \pm i \sqrt{77}$ ; all solution trajectories spiral away from the origin as $t \rightarrow \infty$ .
C) $\lambda=1 \pm i \sqrt{77} ;$ the origin is a saddle.
D) $\lambda=-1 \pm i \sqrt{77}$ ; all solution trajectories spiral toward the origin as $t \rightarrow \infty$ .
E) $\lambda=-1 \pm i \sqrt{77}$ ; all solution trajectories spiral away from the origin as $t \rightarrow \infty$ .