Solved

Consider the First-Order Homogeneous System of Linear Differential Equations
x(t)=ψ−1(t)C \mathbf{x}(t)=\psi^{-1}(t) \mathbf{C}

Question 22

Multiple Choice

Consider the first-order homogeneous system of linear differential equations
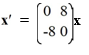
Consider the first-order homogeneous system of linear differential equations Given a fundamental matrix (t) for the system, which of these is the general solution of this system? Here, is an arbitrary constant vector. A) \mathbf{x}(t) =\psi^{-1}(t) \mathbf{C} B) x(t) =\psi(t) \mathbf{C} C) \mathbf{x}(t) =\psi(0) \mathbf{C} D) \mathbf{x}(t) =\psi(t) +C
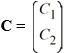Given a fundamental matrix Consider the first-order homogeneous system of linear differential equations Given a fundamental matrix (t) for the system, which of these is the general solution of this system? Here, is an arbitrary constant vector. A) \mathbf{x}(t) =\psi^{-1}(t) \mathbf{C} B) x(t) =\psi(t) \mathbf{C} C) \mathbf{x}(t) =\psi(0) \mathbf{C} D) \mathbf{x}(t) =\psi(t) +C (t) for the system, which of these is the general solution of this system?
Here, Consider the first-order homogeneous system of linear differential equations Given a fundamental matrix (t) for the system, which of these is the general solution of this system? Here, is an arbitrary constant vector. A) \mathbf{x}(t) =\psi^{-1}(t) \mathbf{C} B) x(t) =\psi(t) \mathbf{C} C) \mathbf{x}(t) =\psi(0) \mathbf{C} D) \mathbf{x}(t) =\psi(t) +C is an arbitrary constant vector.


A) x(t) =ψ−1(t) C \mathbf{x}(t) =\psi^{-1}(t) \mathbf{C}
B) x(t) =ψ(t) C x(t) =\psi(t) \mathbf{C}
C) x(t) =ψ(0) C \mathbf{x}(t) =\psi(0) \mathbf{C}
D) x(t) =ψ(t) +C \mathbf{x}(t) =\psi(t) +C

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q17: Consider the first-order homogeneous system of linear

Q18: Compute: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt=" Compute:

Q19: Consider the first-order nonhomogeneous system of

Q20: Consider the first-order homogeneous system of linear

Q21: Consider the first-order homogeneous system of linear

Q23: Consider the first-order homogeneous system of linear

Q24: Consider the first-order homogeneous system of

Q25: Consider the first-order homogeneous system of

Q26: Consider the first-order homogeneous system of linear

Q27: Consider the first-order homogeneous system of