Multiple Choice
Consider the first-order homogeneous system of linear differential equations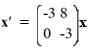
Which of these is the fundamental matrix 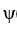 (t) for this system?
(t) for this system?
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Q48: Consider this system of first-order differential
Q49: Consider the first-order homogeneous system of linear
Q50: Consider the following system of linear equations:<br>
Q51: Consider the first-order homogeneous system of linear
Q52: Consider the first-order nonhomogeneous initial value
Q54: Into which of the following systems
Q55: Express the following third-order nonhomogeneous differential equation
Q56: Consider the first-order nonhomogeneous initial value
Q57: Consider the following system of linear equations:<br>
Q58: Consider a system of homogeneous first-order