Multiple Choice
Consider the first-order nonhomogeneous initial value problem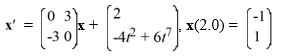
Which of these is the fundamental matrix 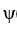 (t) for this system?
(t) for this system?
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Q47: Consider these matrices:<br>D = <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q48: Consider this system of first-order differential
Q49: Consider the first-order homogeneous system of linear
Q50: Consider the following system of linear equations:<br>
Q51: Consider the first-order homogeneous system of linear
Q53: Consider the first-order homogeneous system of
Q54: Into which of the following systems
Q55: Express the following third-order nonhomogeneous differential equation
Q56: Consider the first-order nonhomogeneous initial value
Q57: Consider the following system of linear equations:<br>