Solved

Consider the First-Order Nonhomogeneous Initial Value Problem

Given a Fundamental

Question 56

Multiple Choice

Consider the first-order nonhomogeneous initial value problem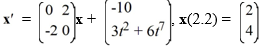
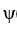Consider the first-order nonhomogeneous initial value problem Given a fundamental matrix (t) for the system, what is the solution of this initial value problem? A) \quad \mathbf{x}(t) =\psi(t) \psi^{-1}(2.2) \left(\begin{array}{l}2 \\ 4\end{array}\right) +\psi(t) \int_{2.2}^{t} \psi^{-1}(s) { }_{3 s^{2}+6 s^{7}}^{-10} d s B) \mathbf{x}(t) =\psi(2.2) \left(\begin{array}{l}2 \\ 4\end{array}\right) +\psi(t) \int_{2.2}^{t} \psi^{-1}(s) { }_{3 s^{2}+6 s^{7}}^{-10} d s C) \mathbf{x}(t) =\psi^{-1}(2.2) \left(\begin{array}{l}2 \\ 4\end{array}\right) +\psi(t) \int_{2.2}^{t} \psi^{-1}(s) { }_{3 s^{2}+6 s^{7}}^{-10} d s D) \mathbf{x}(t) =\psi^{-1}(2.2) \left(\begin{array}{l}2 \\ 4\end{array}\right) +\psi(2.2) \int_{2.2}^{t} \psi^{-1}(s) =-10
Given a fundamental matrix Consider the first-order nonhomogeneous initial value problem Given a fundamental matrix (t) for the system, what is the solution of this initial value problem? A) \quad \mathbf{x}(t) =\psi(t) \psi^{-1}(2.2) \left(\begin{array}{l}2 \\ 4\end{array}\right) +\psi(t) \int_{2.2}^{t} \psi^{-1}(s) { }_{3 s^{2}+6 s^{7}}^{-10} d s B) \mathbf{x}(t) =\psi(2.2) \left(\begin{array}{l}2 \\ 4\end{array}\right) +\psi(t) \int_{2.2}^{t} \psi^{-1}(s) { }_{3 s^{2}+6 s^{7}}^{-10} d s C) \mathbf{x}(t) =\psi^{-1}(2.2) \left(\begin{array}{l}2 \\ 4\end{array}\right) +\psi(t) \int_{2.2}^{t} \psi^{-1}(s) { }_{3 s^{2}+6 s^{7}}^{-10} d s D) \mathbf{x}(t) =\psi^{-1}(2.2) \left(\begin{array}{l}2 \\ 4\end{array}\right) +\psi(2.2) \int_{2.2}^{t} \psi^{-1}(s) =-10 (t) for the system, what is the solution of this initial value problem?


A) x(t) =ψ(t) ψ−1(2.2) (24) +ψ(t) ∫2.2tψ−1(s) 3s2+6s7−10ds \quad \mathbf{x}(t) =\psi(t) \psi^{-1}(2.2) \left(\begin{array}{l}2 \\ 4\end{array}\right) +\psi(t) \int_{2.2}^{t} \psi^{-1}(s) { }_{3 s^{2}+6 s^{7}}^{-10} d s
B) x(t) =ψ(2.2) (24) +ψ(t) ∫2.2tψ−1(s) 3s2+6s7−10ds \mathbf{x}(t) =\psi(2.2) \left(\begin{array}{l}2 \\ 4\end{array}\right) +\psi(t) \int_{2.2}^{t} \psi^{-1}(s) { }_{3 s^{2}+6 s^{7}}^{-10} d s
C) x(t) =ψ−1(2.2) (24) +ψ(t) ∫2.2tψ−1(s) 3s2+6s7−10ds \mathbf{x}(t) =\psi^{-1}(2.2) \left(\begin{array}{l}2 \\ 4\end{array}\right) +\psi(t) \int_{2.2}^{t} \psi^{-1}(s) { }_{3 s^{2}+6 s^{7}}^{-10} d s
D) x(t) =ψ−1(2.2) (24) +ψ(2.2) ∫2.2tψ−1(s) =−10 \mathbf{x}(t) =\psi^{-1}(2.2) \left(\begin{array}{l}2 \\ 4\end{array}\right) +\psi(2.2) \int_{2.2}^{t} \psi^{-1}(s) =-10

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q51: Consider the first-order homogeneous system of linear

Q52: Consider the first-order nonhomogeneous initial value

Q53: Consider the first-order homogeneous system of

Q54: Into which of the following systems

Q55: Express the following third-order nonhomogeneous differential equation

Q57: Consider the following system of linear equations:<br>

Q58: Consider a system of homogeneous first-order

Q59: Consider the first-order nonhomogeneous initial value problem<br>

Q60: Consider the first-order homogeneous system of linear

Q61: Consider the first-order nonhomogeneous initial value