Solved

Consider This Initial-Value Problem:

Question 26

Essay

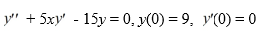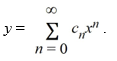Consider this initial-value problem: Consider this initial-value problem: . Assume a solution of this equation can be represented as a power series . Write down the values of these coefficients: C<sub>0</sub> = ________, C<sub>1</sub> = ________, C<sub>2</sub> = ________, C<sub>3</sub> = ________, C<sub>4</sub> = ________, C<sub>5</sub> = ________, C<sub>6</sub> = ________ .
Assume a solution of this equation can be represented as a power series Consider this initial-value problem: . Assume a solution of this equation can be represented as a power series . Write down the values of these coefficients: C<sub>0</sub> = ________, C<sub>1</sub> = ________, C<sub>2</sub> = ________, C<sub>3</sub> = ________, C<sub>4</sub> = ________, C<sub>5</sub> = ________, C<sub>6</sub> = ________ .
Write down the values of these coefficients:
C0 = ________,
C1 = ________,
C2 = ________,
C3 = ________,
C4 = ________,
C5 = ________,
C6 = ________

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q21: Find the general solution of the

Q22: Consider the second-order differential equation <img

Q23: Consider the second-order differential equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"

Q24: Find the general solution of the

Q25: Consider the second-order differential equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"

Q27: Consider the second-order differential equation <img

Q28: Consider the Bessel equation of order

Q29: Consider the second-order differential equation: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"

Q30: What is the greatest lower bound

Q31: Consider the second-order differential equation <img