Consider the Bessel Equation of Order $\neq$ 0
Which of These Is the Recurrence Relation for the Method

Multiple Choice

Consider the Bessel equation of order .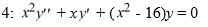
Suppose the method of Frobenius is used to determine a power series solution of the form .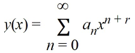
Of this differential equation. Assume a₀ $\neq$ 0.
Which of these is the recurrence relation for the coefficients?

A) $a_{1}=0, a_{n+2}=\frac{-a_{n}}{(r+n-2) ^{2}+16}, n \geq 0$
B) $a_{1}=0, a_{n+2}=\frac{-a_{n}}{(r+n+2) ^{2}-16}, n \geq 0$
C) $a_{1}=1, a_{n+2}=\frac{-a_{n}}{(r+n-2) ^{2}+16}, n \geq 0$
D) $a_{1}=1, a_{n+2}=\frac{-a_{n}}{(r+n+2) ^{2}-16}, n \geq 0$