Short Answer
Consider the second-order differential equation 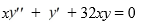 .
.
Suppose the method of Frobenius is used to determine a power series solution of this equation. The indicial equation has r = 0 as a double root. So, one of the solutions can be represented as the power series 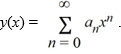 . Assume a0 ≠ 0.
. Assume a0 ≠ 0.
Assuming that a0= 1, one solution of the given differential equation is 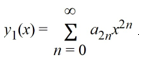
Assuming that 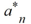 are known, what is the radius of convergence of the power series of the second solution Y2 (x)?
are known, what is the radius of convergence of the power series of the second solution Y2 (x)?
Correct Answer:

Verified
Correct Answer:
Verified
Q18: What is the Taylor series expansion for
Q19: Consider the second-order differential equation <img
Q20: Which of these power series is equivalent
Q21: Find the general solution of the
Q22: Consider the second-order differential equation <img
Q24: Find the general solution of the
Q25: Consider the second-order differential equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg"
Q26: Consider this initial-value problem: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TBW1042/.jpg" alt="Consider
Q27: Consider the second-order differential equation <img
Q28: Consider the Bessel equation of order