Multiple Choice
A portion of the direction field for the differential equation 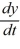 = f(y) is shown below:
= f(y) is shown below: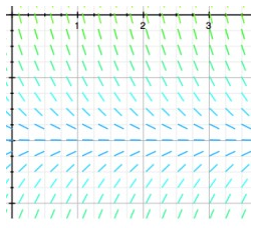
The dotted horizontal line has equation y = -7. Which of the following statements are true? Select all that apply.
A) y(t) = 0 is the solution to the initial-value problem 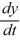 = f(y) , y(0) = 0.
= f(y) , y(0) = 0.
B) y(t) = -7 is the only equilibrium solution.
C) There is no solution of the initial-value problem 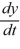 = f(y) , y(0) =
= f(y) , y(0) = 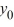 when
when 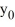 = -7.
= -7.
D) Every solution curve y(t) is increasing toward a negative limit as t .
E) Every solution curve y(t) tends towards -7 as t .
F) F(y) cannot be a linear function of y.
Correct Answer:

Verified
Correct Answer:
Verified
Q2: Newton's Law of Cooling states that the
Q3: A model for the vertical flight of
Q4: For what values of r is y(t)
Q5: An antibiotic is being administered intravenously to
Q6: Which of the following are solutions to
Q7: Consider the differential equation x = <img
Q8: Which of the following are solutions to
Q9: Eight differential equations and four slope fields
Q10: Which of the following pairs of values
Q11: A model for the vertical flight of