(See Problem 2

Multiple Choice

(See Problem 2.) Willy's only source of wealth is his chocolate factory. He has the utility function 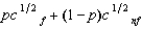, where p is the probability of a flood, 1 - p is the probability of no flood, and c_f and c_nf are his wealth contingent on a flood and on no flood, respectively. The probability of a flood is p = . The value of Willy's factory is $500,000 if there is no flood and 0 if there is a flood. Willy can buy insurance where if he buys $x worth of insurance, he must pay the insurance company $ 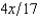whether there is a flood or not, but he gets back $x from the company if there is a flood. Willy should buy

A) enough insurance so that if there is a flood, after he collects his insurance, his wealth will be the same whether there is a flood or not.
B) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there is no flood.
C) no insurance since the cost per dollar of insurance exceeds the probability of a flood.
D) .enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there is no flood.
E) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there is no flood