When Estimating Y = β₀ + β₁x₁ + β₂x₂

Multiple Choice

When estimating y = β₀ + β₁x₁ + β₂x₂ + β₃x₃ + ε, you wish to test H₀: β₁ = β₂ = 0 versus 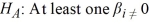. The value of the test statistic is F_(2,20) = 2.50 and its associated p-value is 0.1073. At the 5% significance level, the conclusion is to ________.

A) reject the null hypothesis; we can conclude that x₁ and x₂ are jointly significant
B) reject the null hypothesis; we cannot conclude that x₁ and x₂ are jointly significant
C) not reject the null hypothesis; we can conclude that x₁ and x₂ are jointly significant
D) not reject the null hypothesis; we cannot conclude that x₁ and x₂ are jointly significant