Multiple Choice
The following data show the demand for an airline ticket dependent on the price of this ticket. 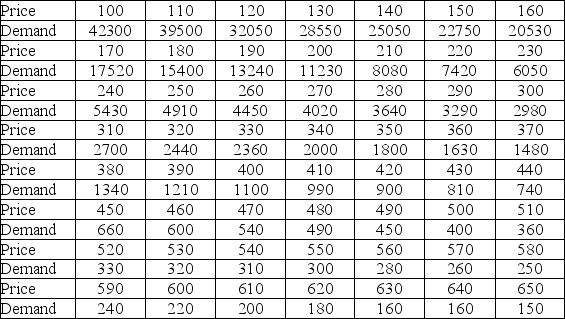 For the assumed cubic and log-log regression models, Demand = β0 + β1Price + β2Price2 + β3Price3 + ε and ln(Demand) = β0 + β1ln(Price) + ε, the following regression results are available.
For the assumed cubic and log-log regression models, Demand = β0 + β1Price + β2Price2 + β3Price3 + ε and ln(Demand) = β0 + β1ln(Price) + ε, the following regression results are available.  Assuming that the sample correlation coefficient between Demand and
Assuming that the sample correlation coefficient between Demand and 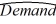 = exp(26.3660 - 3.2577 ln(Price) + (0.2071) 2/2) is 0.956, what is the predicted demand for a price of $250 found by the model with better fit?
= exp(26.3660 - 3.2577 ln(Price) + (0.2071) 2/2) is 0.956, what is the predicted demand for a price of $250 found by the model with better fit?
A) 4,447.88
B) 3,914.38
C) 4,029.38
D) 5,175.09
Correct Answer:

Verified
Correct Answer:
Verified
Q102: It is believed that the sales volume
Q103: Thirty employed single individuals were randomly selected
Q104: Thirty employed single individuals were randomly selected
Q105: The regression model ln(y) = β<sub>0</sub> +
Q106: For the log-log model ln(y) = β<sub>0</sub>
Q108: In the model ln(y) = β<sub>0</sub> +
Q109: Typically, the sales volume declines with an
Q110: The following data, with the corresponding Excel
Q111: It is believed that the sales volume
Q112: The following scatterplot shows productivity and number