To Examine the Differences Between Salaries of Male and Female

Multiple Choice

To examine the differences between salaries of male and female middle managers of a large bank, 90 individuals were randomly selected, and two models were created with the following variables considered: Salary = the monthly salary (excluding fringe benefits and bonuses) ,
Educ = the number of years of education,
Exper = the number of months of experience,
Train = the number of weeks of training,
Gender = the gender of an individual; 1 for males, and 0 for females.
Excel partial outputs corresponding to these models are available and shown below.
Model A: Salary = β₀ + β₁Educ + β₂Exper + β₃Train + β₄Gender + ε 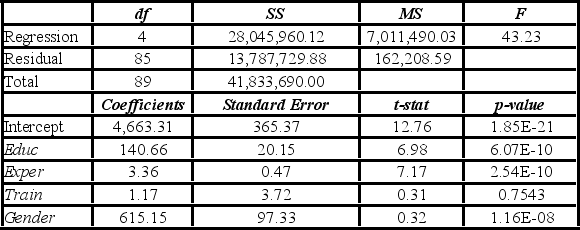Model B: Salary = β₀ + β₁Educ + β₂Exper + β₃Gender + ε 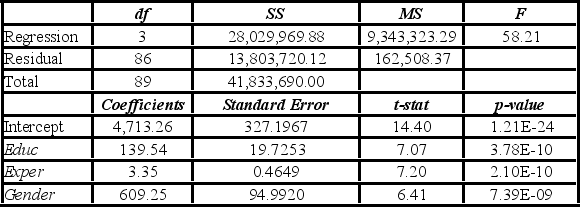Assuming the same years of education and months of experience, what is the null hypothesis for testing whether the mean salary of males is greater than the mean salary of females using Model B?

A) H₀: β₃ ≤ 0
B) H₀: β₃ ≥ 0
C) H₀: β₃> 0
D) H₀: β₃ = 0