Multiple Choice
Select the graph that represents the given conic section. If the conic is a parabola, specify (using rectangular coordinates) the vertex and directrix. If the conic is an ellipse, specify the center, the eccentricity, and the lengths of the major and minor axes. If the conic is a hyperbola, specify the center, the eccentricity, and the lengths of the transverse and conjugate axes.
A) 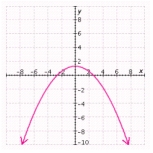 Vertex: Directrix:
Vertex: Directrix:
B) 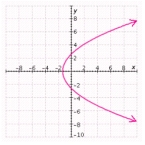 Vertex: Directrix:
Vertex: Directrix:
C) 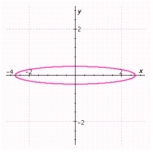 Center: Eccentricity: Major axis length:
Center: Eccentricity: Major axis length:
Minor axis length:
D) 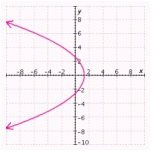 Vertex: Directrix:
Vertex: Directrix:
E) 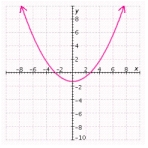 Vertex: Directrix:
Vertex: Directrix:
Correct Answer:

Verified
Correct Answer:
Verified
Q1: Graph the ellipse. Specify the lengths
Q2: Graph the ellipse. Specify the lengths
Q3: Graph the hyperbola. Specify the following:
Q4: Select the answer that represents the
Q6: Use the given information to find
Q7: Use the given information to find
Q8: Find the center and the radius
Q9: Graph the parabola. Specify the focus,
Q10: Find the equation of the tangent
Q11: Suppose the line <span class="ql-formula"