Multiple Choice
Graph the ellipse. Specify the lengths of the major and minor axes, the foci, the center and the eccentricity.
A) center: (- 2, 5) ;
Length of major axis: 6;
Length of minor axis: 4;
Foci: ;
Eccentricity: 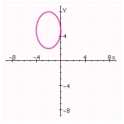
B) center: (1, - 2.5) ;
Length of major axis: 3;
Length of minor axis: 2;
Foci: ;
Eccentricity: 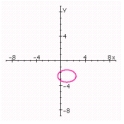
C) center: (2, - 5) ;
Length of major axis: 6;
Length of minor axis: 4;
Foci: ;
Eccentricity:
D) center: (1, - 2.5) ;
Length of major axis: 3;
Length of minor axis: 2;
Foci: ;
Eccentricity: 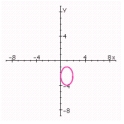
E) center: (2, - 5) ;
Length of major axis: 6;
Length of minor axis: 4;
Foci: ;
Eccentricity: 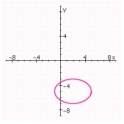
Correct Answer:

Verified
Correct Answer:
Verified
Q2: Graph the ellipse. Specify the lengths
Q3: Graph the hyperbola. Specify the following:
Q4: Select the answer that represents the
Q5: Select the graph that represents the
Q6: Use the given information to find
Q7: Use the given information to find
Q8: Find the center and the radius
Q9: Graph the parabola. Specify the focus,
Q10: Find the equation of the tangent
Q11: Suppose the line <span class="ql-formula"