Imagine We Were Interested in the Effect of Supporters Singing $\quad$

Multiple Choice

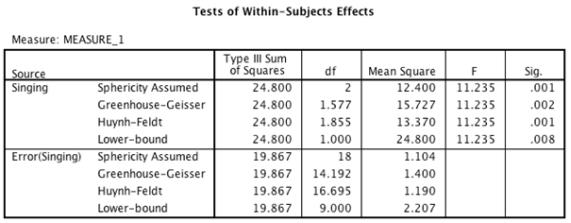
Imagine we were interested in the effect of supporters singing on the number of goals scored by soccer teams. We took 10 groups of supporters of 10 different soccer teams and asked them to attend three home games, one at which they were instructed to sing in support of their team (e.g., ‘Come on, you Reds!’) , one at which they were instructed to sing negative songs towards the opposition (e.g., ‘You’re getting sacked in the morning!’) and one at which they were instructed to sit quietly. The order of chanting was counterbalanced across groups.
- An ANOVA with a simple contrasts using the last category as a reference was conducted. Looking at the output tables below, what does the first contrast (Level 1 vs. Level 3) compare? $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ $\quad$ Tests of Within-Subjects Contrasts
Measure: MEASURE_1
$\begin{array}{|ll|r|r|r|r|r|}\hline\text { Source } & \text { Sinqing } & \begin{array}{r}\text { Type IIl Sum } \\\text { of Squares }\end{array} &{\text { df }} & \text { Mean Square } & {\text { F }} & {\text { Sig. }} \\\hline \text { Singing } & \text { Level 1 vs. Level 3 } & 19.600 & 1 & 19.600 & 7.230 & .025 \\& \text { Level 2 vs. Level 3 } & 6.400 & 1 & 6.400 & 6.000 & .037 \\\hline \text { Error(Singing) } & \text { Level 1 vs. Level 3 } & 24.400 & 9 & 2.711 & & \\& \text { Level 2 vs. Level 3 } & 9.600 & 9 & 1.067 & &\\\hline \end{array}$

A) Positive singing vs.no singing
B) No singing vs.negative singing
C) Negative singing vs.positive singing
D) We cannot tell which groups the levels represent from this output.