At the Stock and Watson (Http://www

Essay

At the Stock and Watson (http://www.pearsonhighered.com/stock_watson)website go to Student Resources and select the option "Datasets for Replicating Empirical Results." Then select the "California Test Score Data Used in Chapters 4-9" (caschool.xls)and open it in a spreadsheet program such as Excel.
In this exercise you will estimate various statistics of the Linear Regression Model with One Regressor through construction of various sums and ratio within a spreadsheet program.
Throughout this exercise,let Y correspond to Test Scores (testscore)and X to the Student Teacher Ratio (str).To generate answers to all exercises here,you will have to create seven columns and the sums of five of these.They are
(i)Yi, (ii)Xi, (iii)(Yi- ), (iv)(Xi- 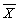), (v)(Yi- 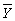)×(Xi- 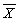), (vi)(Xi- 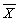)2, (vii)(Yi- 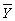)2
Although neither the sum of (iii)or (iv)will be required for further calculations,you may want to generate these as a check (both have to sum to zero).
a.Use equation (4.7)and the sums of columns (v)and (vi)to generate the slope of the regression.
b.Use equation (4.8)to generate the intercept.
c.Display the regression line (4.9)and interpret the coefficients.
d.Use equation (4.16)and the sum of column (vii)to calculate the regression R2.
e.Use equation (4.19)to calculate the SER.
f.Use the "Regression" function in Excel to verify the results.