Essay
In a simple regression with an intercept and a single explanatory variable,the variation in Y 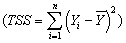 can be decomposed into the explained sums of squares
can be decomposed into the explained sums of squares 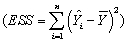 and the sum of squared residuals
and the sum of squared residuals 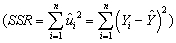 (see,for example,equation (4.35)in the textbook).
(see,for example,equation (4.35)in the textbook).
Consider any regression line,positively or negatively sloped in {X,Y} space.Draw a horizontal line where,hypothetically,you consider the sample mean of Y 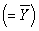 to be.Next add a single actual observation of Y.
to be.Next add a single actual observation of Y.
In this graph,indicate where you find the following distances: the
(i)residual
(ii)actual minus the mean of Y
(iii)fitted value minus the mean of Y
Correct Answer:

Verified
Correct Answer:
Verified
Q29: To decide whether or not the slope
Q36: The reason why estimators have a sampling
Q39: Imagine that you had discovered a relationship
Q40: (Requires Appendix material)At a recent county fair,you
Q41: (Requires Calculus)Consider the following model:<br>Yi = β1Xi
Q43: Interpreting the intercept in a sample regression
Q45: The neoclassical growth model predicts that for
Q46: Assume that you have collected a sample
Q47: At the Stock and Watson (http://www.pearsonhighered.com/stock_watson)website go
Q52: The OLS slope estimator is not defined