Exam 22: Linear Programming: The Simplex Method
Exam 1: Introduction to Quantitative Analysis71 Questions
Exam 2: Probability Concepts and Applications157 Questions
Exam 3: Decision Analysis128 Questions
Exam 4: Regression Models133 Questions
Exam 5: Forecasting111 Questions
Exam 6: Inventory Control Models123 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods110 Questions
Exam 8: Linear Programming Applications105 Questions
Exam 9: Transportation,assignment,and Network Models98 Questions
Exam 10: Integer Programming,goal Programming,and Nonlinear Programming98 Questions
Exam 11: Project Management134 Questions
Exam 12: Waiting Lines and Queuing Theory Models145 Questions
Exam 13: Simulation Modeling79 Questions
Exam 14: Markov Analysis86 Questions
Exam 15: Statistical Quality Control98 Questions
Exam 16: Analytic Hierarchy Process53 Questions
Exam 17: Dynamic Programming67 Questions
Exam 18: Decision Theory and the Normal Distribution50 Questions
Exam 19: Game Theory47 Questions
Exam 20: Mathematical Tools: Determinants and Matrices99 Questions
Exam 21: Calculus-Based Optimization24 Questions
Exam 22: Linear Programming: The Simplex Method100 Questions
Exam 23: Transportation, Assignment, and Network Algorithms111 Questions
Select questions type
Table M7-3 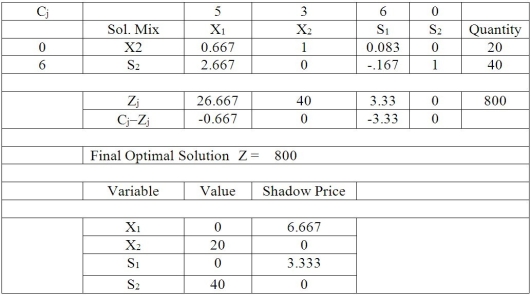 -According to Table M7-3,which is the final simplex tableau for a linear programming problem (maximization),what would happen to profits if the X1 column were selected as the pivot column and another iteration of the simplex algorithm were performed?
-According to Table M7-3,which is the final simplex tableau for a linear programming problem (maximization),what would happen to profits if the X1 column were selected as the pivot column and another iteration of the simplex algorithm were performed?
(Multiple Choice)
5.0/5  (37)
(37)
If,at an optimal solution,the Cj - Zj value for a real variable that is not in the solution mix has a value of one,there are multiple optimal solutions.
(True/False)
4.8/5  (32)
(32)
Consider the following general form of a linear programming problem: Maximize Profit
Subject to: Amount of resource A used ≤ 100 units
Amount of resource B used ≤ 240 units
Amount of resource C used ≤ 50 units
The shadow price for S1 is 25,for S2 is 0,and for S3 is 40.If the right-hand side of constraint 3 were changed from 150 to 151,what would happen to maximum possible profit?
(Multiple Choice)
4.7/5  (33)
(33)
In a maximization problem,if a variable is to enter the solution,it must have a positive coefficient in the Cj - Zj row.
(True/False)
4.9/5  (31)
(31)
In applying the simplex solution procedure to a minimization problem to determine which variable enters the solution mix,
(Multiple Choice)
4.8/5  (38)
(38)
Solve the following linear programming problem using the simplex method.
Maximize 3 X1 + 5X2
Subject to: 4 X1 + 3 X2 ≤ 48
X1 + 2 X2 ≤ 20
X1,X2 ≥ 0
(Essay)
4.8/5  (27)
(27)
How does Karmarkar's Algorithm differ from the simplex method?
(Multiple Choice)
4.8/5  (29)
(29)
Sensitivity testing of basic variables involves reworking the initial simplex tableau.
(True/False)
4.9/5  (30)
(30)
Consider the following linear program:
Maximize Z = 3 X1 + 2 X2 - X3
Subject to: X1+ X2 + 2 X3 ≤ 10
2 X1 - X2 + X3 ≤ 20
3 X1 + X2 ≤ 15
X1,X2,X3 ≥ 0
(a)Convert the above constraints to equalities by adding the appropriate slack variables.
(b)Set up the initial simplex tableau and solve.
(Essay)
4.7/5  (40)
(40)
As we are doing the ratio calculations for a simplex iteration,if there is a tie for the smallest ratio,the problem is degenerate.
(True/False)
4.8/5  (40)
(40)
Sensitivity analyses are used to examine the effects of changes in
(Multiple Choice)
4.8/5  (39)
(39)
In linear programs with more than two decision variables,the area of feasible solutions is represented by an n-dimensional polyhedron.
(True/False)
4.8/5  (33)
(33)
Write the dual of the following linear program:
Maximize 3 X1 + 5X2
Subject to: 4 X1 + 2 X2 ≤ 44
X1 + 2 X2 ≤ 24
X1,X2 ≥ 0
(Essay)
4.7/5  (29)
(29)
The number -2 in the X2 column and X1 row of a simplex tableau implies that
(Multiple Choice)
4.8/5  (34)
(34)
For a maximization problem,the Zj values in the body of the simplex table represent the gross profit given up by adding one unit of this variable into the current solution.
(True/False)
4.7/5  (36)
(36)
Table M7-2 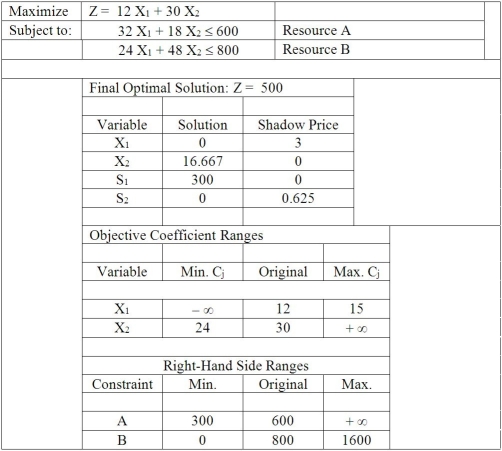 -According to Table M7-2,which is a summarized solution output from simplex analysis,if the amount of resource A were decreased so that there were only 550 units available instead of 600,what would happen to total profits?
-According to Table M7-2,which is a summarized solution output from simplex analysis,if the amount of resource A were decreased so that there were only 550 units available instead of 600,what would happen to total profits?
(Multiple Choice)
4.9/5  (31)
(31)
Showing 41 - 60 of 100
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)