Exam 8: The Nature of Measurement
Exam 1: The Nature of Problem Solving53 Questions
Exam 2: The Nature of Sets64 Questions
Exam 3: The Nature of Logic160 Questions
Exam 4: The Nature of Numeration Systems102 Questions
Exam 5: The Nature of Numbers139 Questions
Exam 6: The Nature of Algebra173 Questions
Exam 7: The Nature of Geometry139 Questions
Exam 8: The Nature of Measurement50 Questions
Exam 9: The Nature of Networks and Graph Theory76 Questions
Exam 10: The Nature of Growth57 Questions
Exam 11: The Nature of Sequences, Series, and Financial Management130 Questions
Exam 12: The Nature of Counting78 Questions
Exam 13: The Nature of Probability97 Questions
Exam 14: The Nature of Statistics82 Questions
Exam 15: The Nature of Graphs and Functions74 Questions
Exam 16: The Nature of Mathematical Systems97 Questions
Exam 17: The Nature of Voting and Apportionment52 Questions
Select questions type
Group the objects into classes so that all the elements within each class are topologically equivalent and no elements from different classes are topologically equivalent.
A) a bolt
B) a straw
C) a sewing needle
D) a funnel with a handle
(Short Answer)
5.0/5  (38)
(38)
The map in figure shows driving distances and times between California and Nevada cities. Use Kruskal's algorithm to find the minimum spanning tree for the following cities: Santa Rosa, San Francisco, Oakland, Manteca, Yosemite Village, Merced, Fresno, and San Jose. 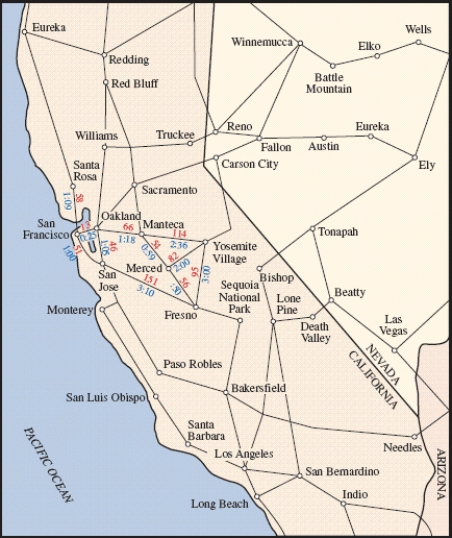 __________ mi
__________ mi
(Short Answer)
4.8/5  (34)
(34)
A saleswoman wants to visit eastern cities, New York City, Boston, Cleveland, and Washington, D.C. Driving distances are as shown in the figure below. What is the shortest trip starting in New York that visits each of these cities, if 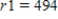 ,
, 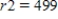 ? Find a solution using the brute-force method.
? Find a solution using the brute-force method. 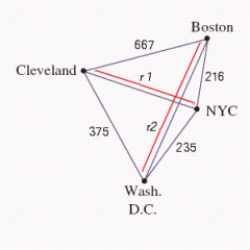
(Multiple Choice)
4.7/5  (40)
(40)
The map in figure shows driving distances and times between California and Nevada cities. Use Kruskal's algorithm to find the minimum spanning tree for the following cities: Santa Rosa, San Francisco, Oakland, Manteca, Yosemite Village, Merced, Fresno, and San Jose. 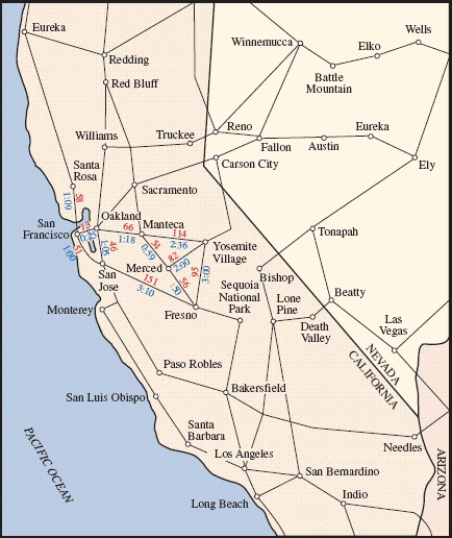
(Multiple Choice)
4.8/5  (37)
(37)
On a planet far, far away, Luke finds himself in a strange building with hexagon-shaped rooms as shown in the figure below. In his search for the princess, he always moves to an adjacent room and always in a southerly direction. How many paths are there to room 1?
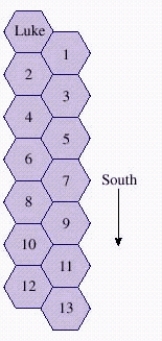
__________ path0
__________ path0
(Short Answer)
4.8/5  (27)
(27)
Can you pass the floor plan in through all the rooms while going through each door only once? 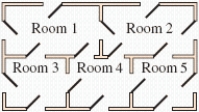 Answer traversable or not traversable.
Answer traversable or not traversable.
(Short Answer)
4.9/5  (40)
(40)
Does the network in d) have a Hamiltonian cycle? If this network has one, describe it. 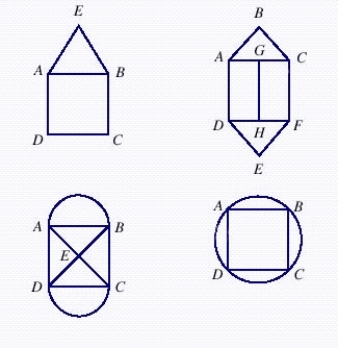
(Multiple Choice)
4.9/5  (41)
(41)
Showing 41 - 50 of 50
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)